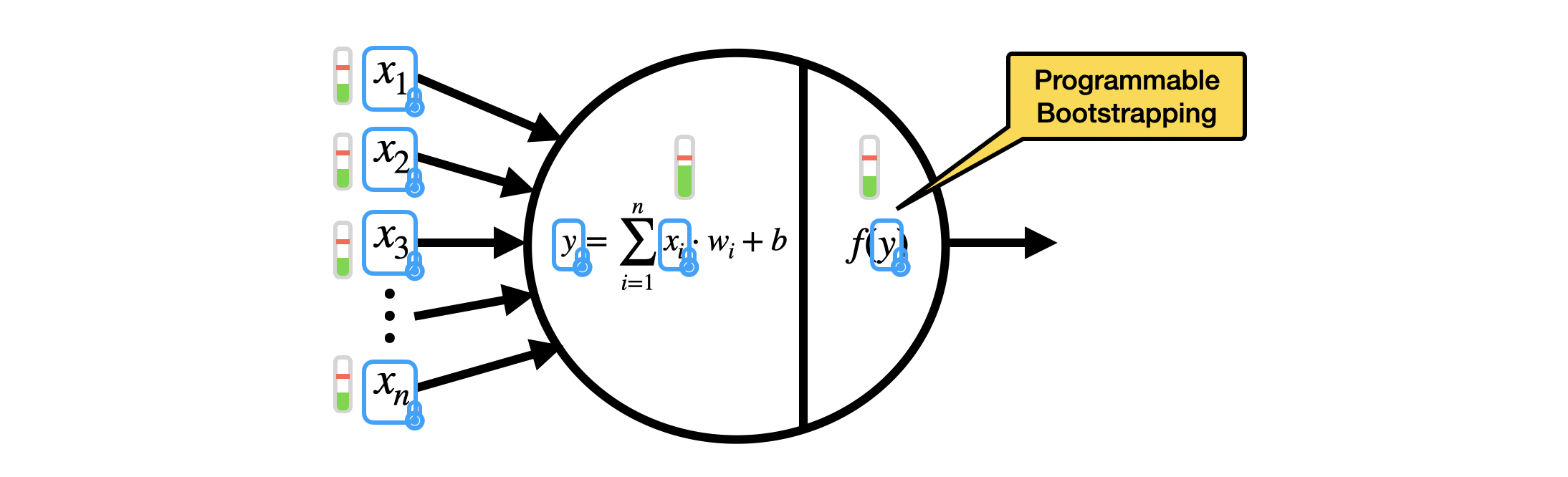
其实是一个 TFHE 随便记记。非常感谢作者 Ilaria Chillotti 的讲解和 FHE_org 让我这种笨比也有机会领会这么高级的 FHE 方案。

Algbra

TFHE 主要自举非常高效且同时可以计算任何函数 ( Torus 主要用在 rounding？)。

FHE 代表全同态加密，T则代表 Torus，环面。只用到一维实数 Torus。~~有没有可能衍伸到环~~

\[\mathbb{T}=\mathbb{R}/\mathbb{Z}=\mathbb{R}\bmod 1\]

所有模 1 实数。如果定义实数加法和整数环上的数乘，$(\mathbb{T},+,\times)$，Torus 是一个 $\mathbb{Z}$-模(~~任何阿贝尔群都是~~)。但它并没有环的结构，实数乘法和模运算不相容：

\[\exists t_1,t_2\in \bar{t_1},\bar{t_2}\colon t_1 \cdot t_2\bmod 1\neq(t_1\bmod 1)\cdot(t_2\bmod 1)\bmod 1\]

$\mathbb{T}_N\bqty{X}$ 表示系数在 $\mathbb{T}$ 里的多项式，模上分圆(~~主要是整系数不可约~~)多项式 $X^N+1$，$N$ 为 2 的幂。$(\mathbb{T}_N\bqty{X},+,\times)$ 是 $\mathfrak{R}=\mathbb{Z}\bqty{X}/(X^N+1)$ 上的模，$\mathbb{T}_N\bqty{X}\bmod(X^N+1)$ 同样可以在 Torus 多项式上进行加法和整数多项式的数乘，但两个 Torus 多项式之间的乘法没有定义。

用 $\mathcal{R}$ 表示多项式环 $\mathbb{Z}\bqty{X}/(X^N+1)$，$\mathcal{R}_q$同理。高斯分布 $\chi_{\mu,\sigma}$。如果 $\mu=0$ 记作 $\chi_\sigma$。

cipherS

用三种密文的原因主要是充分利用每种密文的属性。

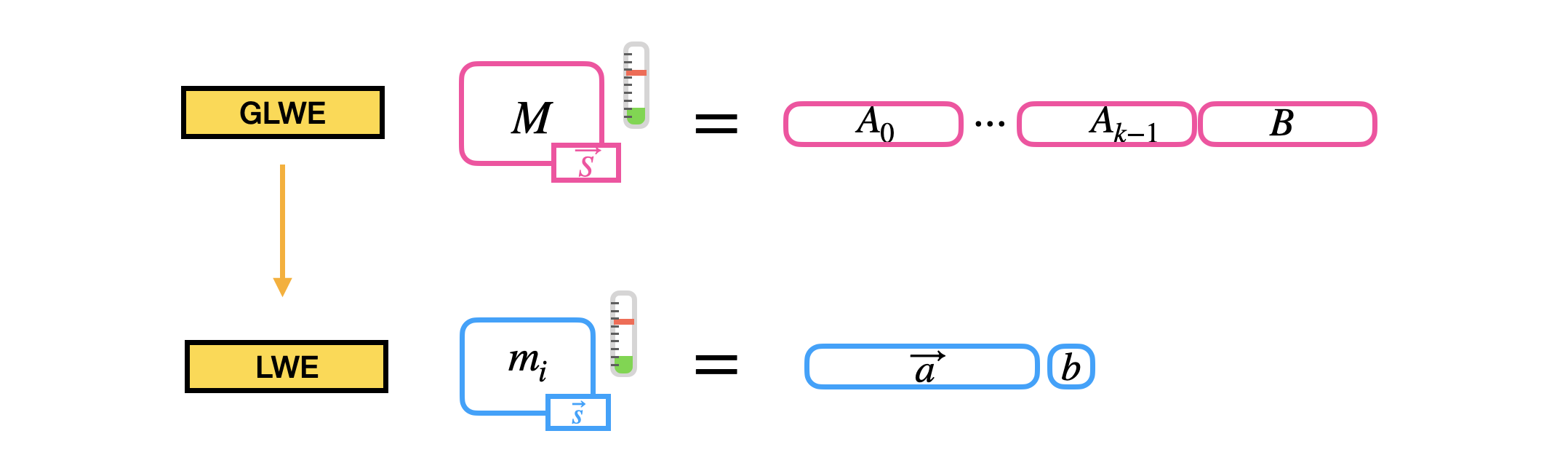
GLWE

yysy，LWE 问题在 FHE 构造里有够被简化。LWE 和 RLWE 加密方式本质上是一样的，LWE 的明文如 $\mathbb{T}$ 可以被加密成多项式 $\mathbb{T}_N\bqty{X}$ 的一个系数。密钥记作 $R$ 里的 $k$ 个随机多项式：(~~多项式用大写字母~~)

\[\vec{S}=\pqty{S_0,\dots,S_{k-1}}\in\mathcal{R}^k\]

里面的 $\mathbb{R}$ 元素可以在均匀随机的二进制分布，三元分布，高斯分布或者均匀分布里采样。对于每种类型的密钥都可以实现特定安全等级的参数。例子是从均匀随机二进制分布采样。

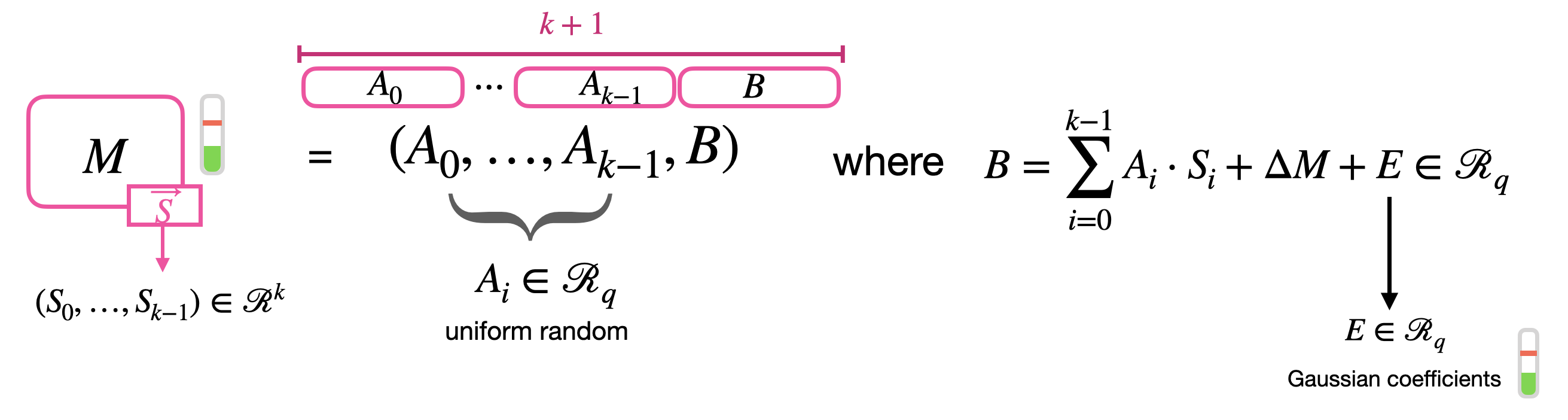
$p,q$ 为两个正整数，一般选为 2 的幂，否则在编码消息，i.e.，$\Delta M$ 时需要 rounding。$p\leq q,\Delta=q/p$。$q$ 一般叫做密文模数，$p$ 叫做明文模数。$\Delta$ 放缩因子 (scaling factor)。对于消息 $M \in \mathcal{R}_p$，其在密钥 $\vec{S}$ 下的密文：

\[(A_0, \ldots, A_{k-1}, B) \in GLWE_{\vec{S}, \sigma}(\Delta M) \subseteq \mathcal{R}_q^{k+1}\]

$A_i$ 均匀随机的在 $\mathcal{R}q$ 采样，$B = \sum_{i=0}^{k-1} A_i \cdot S_i + \Delta M + E \in \mathcal{R}_q$，$E \in \mathcal{R}_q$ 其系数在高斯分布 $\chi{\sigma}$ 中采样。

通常 $\pqty{A_0,\dots,A_{k-1}}$ 叫作 mask，B 叫作 body。多项式 $\Delta M$ 叫作 $M$ 的编码。每次对消息加密都会采样随机数(mask 和 error)，所以每次 (对同样) 消息加密密文都不一样，前文也说过 LWE 安全性取决于其伪随机性。解密就典中典减一减得到 $\Delta M+E$再 rounding。解密要求 $

<\Delta/2$，i.e.，$E$ 的每个系数 $

e_i

<\Delta/2$。

模 $X^N+1$ 利用 $X^N\equiv -1$。

Trival GLWE ciphertexts：

\[(0, \dots, 0, \Delta M) \in \mathcal{R}_{q}^{k+1}\]

用来当成公开参数，公钥就 $M$ 也全是 0 再线性组合。

LWE and RLWE

$k=n\in\mathbb{Z}$(~~为什么要区分 k 跟 n~~) 且 $N=1$ 就得到了 LWE。此时 $\mathcal{R}_q$ (resp. $\mathcal{R}$) 就是 $\mathbb{Z}_q$ (resp. $\mathbb{Z}$)。

$k=1$ 且 $N$ 是 2 的幂就得到了RLWE。(~~为什么要是 2 的幂~~)

GLev

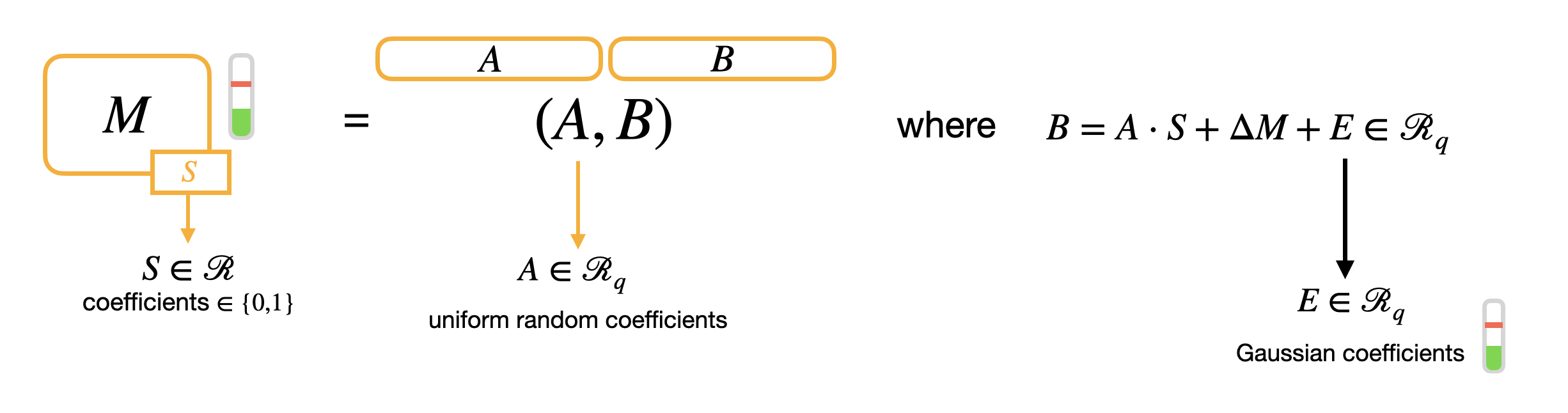
leveled 方案里用的很多。实际上就是用冗余的和精心设计过 $\Delta$ 的 GLWE 加密单个消息 $M$。密文密钥都跟 GLWE 一样。虽然一直在用，但正式命名貌似非常的晚(CLOT21)。$\Delta$ 底为 $\beta$，通常为 2 的幂和层数 $\ell$

\[\left(GLWE_{\vec{S}, \sigma}\left(\frac{q}{\beta^{1}} M\right) \times \ldots \times G L W E_{\vec{S}, \sigma}\left(\frac{q}{\beta^{\ell}} M\right)\right)=G L e v_{\vec{S}, \sigma}^{\beta, \ell}(M) \subseteq \mathcal{R}_{q}^{\ell \cdot(k+1)}\]

$\times$，笛卡儿积。$\beta,q$ 如果不是 2 的幂，编码的时候需要 rounding。解密就对对应 $\Delta$ 的 GLWE 解密 1 次就行。同样的也有 Lev 和 RLev。

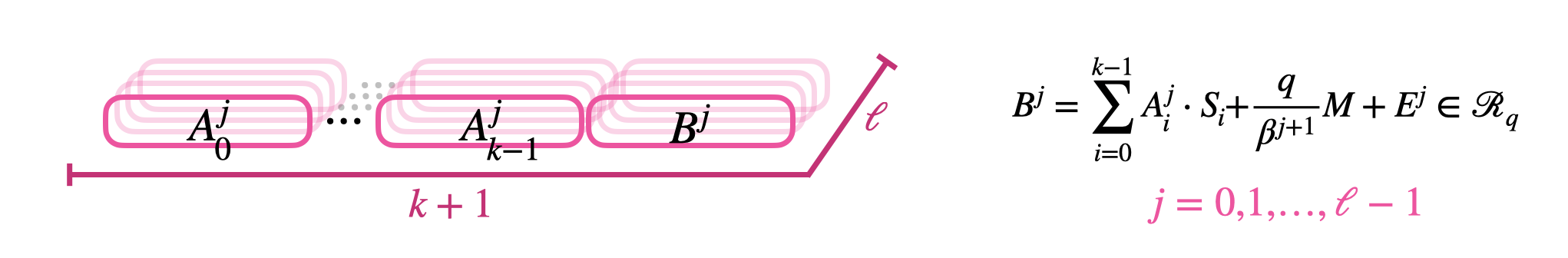
GGSW

说白了就是冗余复读。

GLWE 密文是 $\mathcal{R}_q$ 元素组成的向量(1 维矩阵)。
GLev 密文是 GLWE 密文组成的向量。($\mathcal{R}_q$ 元素组成的 2 维矩阵)
GGSW 密文是 GLev 密文组成的向量。($\mathcal{R}_q$ 元素组成的 3 维矩阵，或 GLWE 密文组成的 2 维矩阵)

\[\left(GLev_{\vec{S}, \sigma}^{\beta, \ell}\left(-S_{0} M\right) \times \ldots \times GLev_{\vec{S}, \sigma}^{\beta, \ell}\left(-S_{k-1} M\right) \times GLev_{\vec{S}, \sigma}^{\beta, \ell}(M)\right)=GGSW_{\vec{S}, \sigma}^{\beta, \ell}(M) \subseteq \mathcal{R}_{q}^{(k+1) \times \ell(k+1)}\]

注意每个 GLev 密文中密钥的 $S_i$ 项和 $M$ 的乘积。密钥 $\vec{S}$ 跟 GLWE 和 GLev 密文相同。解密时对最后一个 GLev 密文解密就够了(~~毕竟 $\Delta$ 最简单。i.e.，对里面任意一个 GLWE 密文解密~~)。GSW 跟 RGSW 与上文同样操作。

Encodings and linear leveled operations

加法数乘就对应元素分别计算，没什么好讲的。数乘的噪音增加跟常数多项式 $\Lambda$ 的系数成比例。数乘大数需要操作，下文会讲。

Encoding integers in the MSB

TFHE 错误编码在 LSB，消息编码在 MSB。一些方案跟他一样，比如 B/FV 和 HEAAN/CKKS。一些反过来，比如 BGV。

GLWE 能支持更多不同的编码方式。

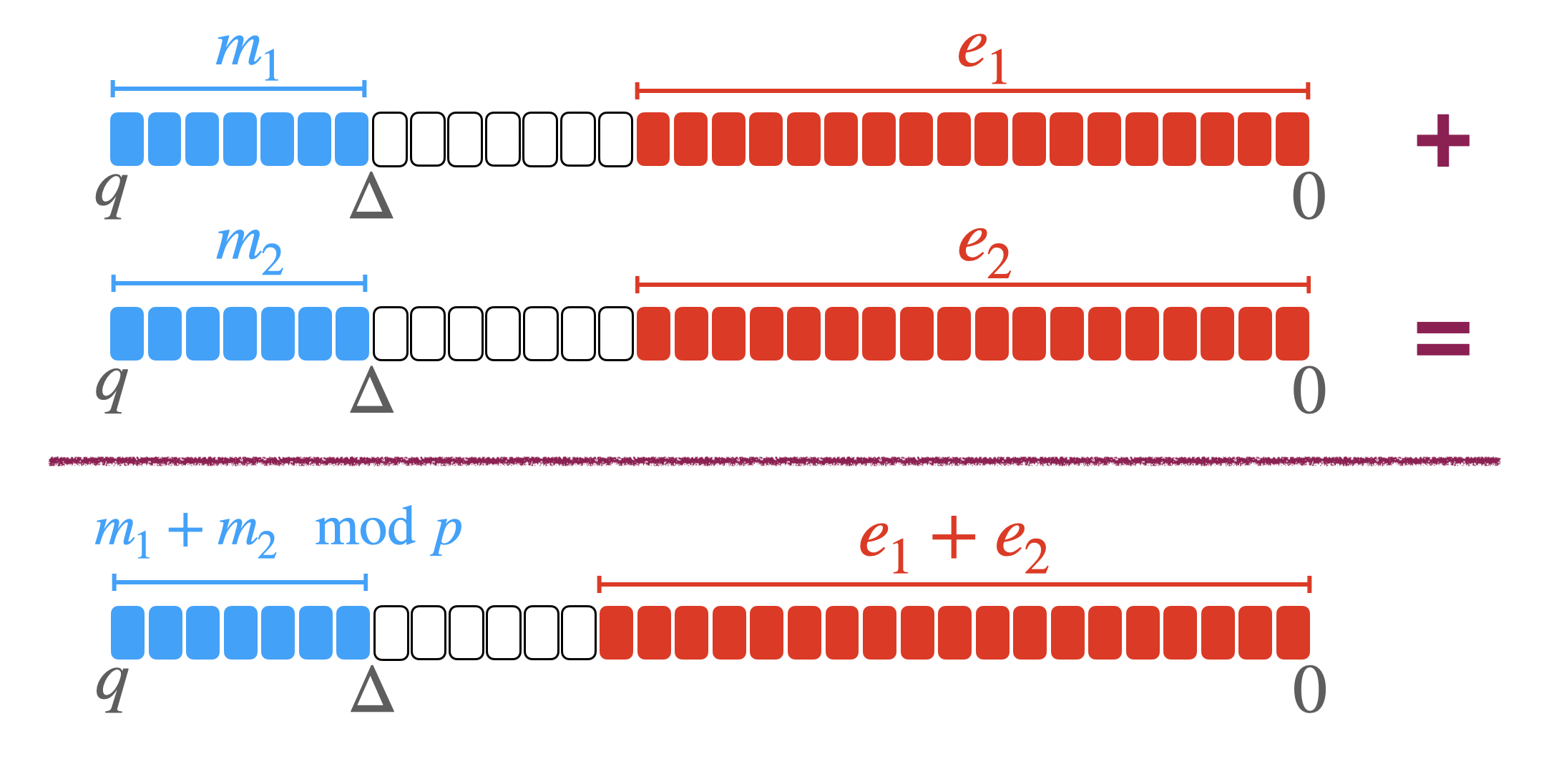
这种编码可以实现模 $p$ 的(leveled operation)分级(~~佛了，原来中文翻译是分级。R18是吧~~)操作(加法和数乘)。比如两个 GLWE 密文用相同的 $\Delta$ 编码在 MSB，加一加结果就是两个明文的模加法，$\Delta$ 不变。当然噪音也加一加，并且还有可能会进位。(~~进位是不是就表示 g 了~~)例子：$q=2^{32},p=2^7,\Delta=2^{25},m\in\mathbb{Z}_p$。

Encoding integers in the MSB with padding bits

编码通常会被我们想实现的全同态操作影响。padding 就是前面空一些给分级操作(加法和数乘)提供空间。例子：$q=2^{32},p=2^7,\Delta=2^{25},p’=2^5,m\in\mathbb{Z}_p’$。也就是有 2 bit padding。

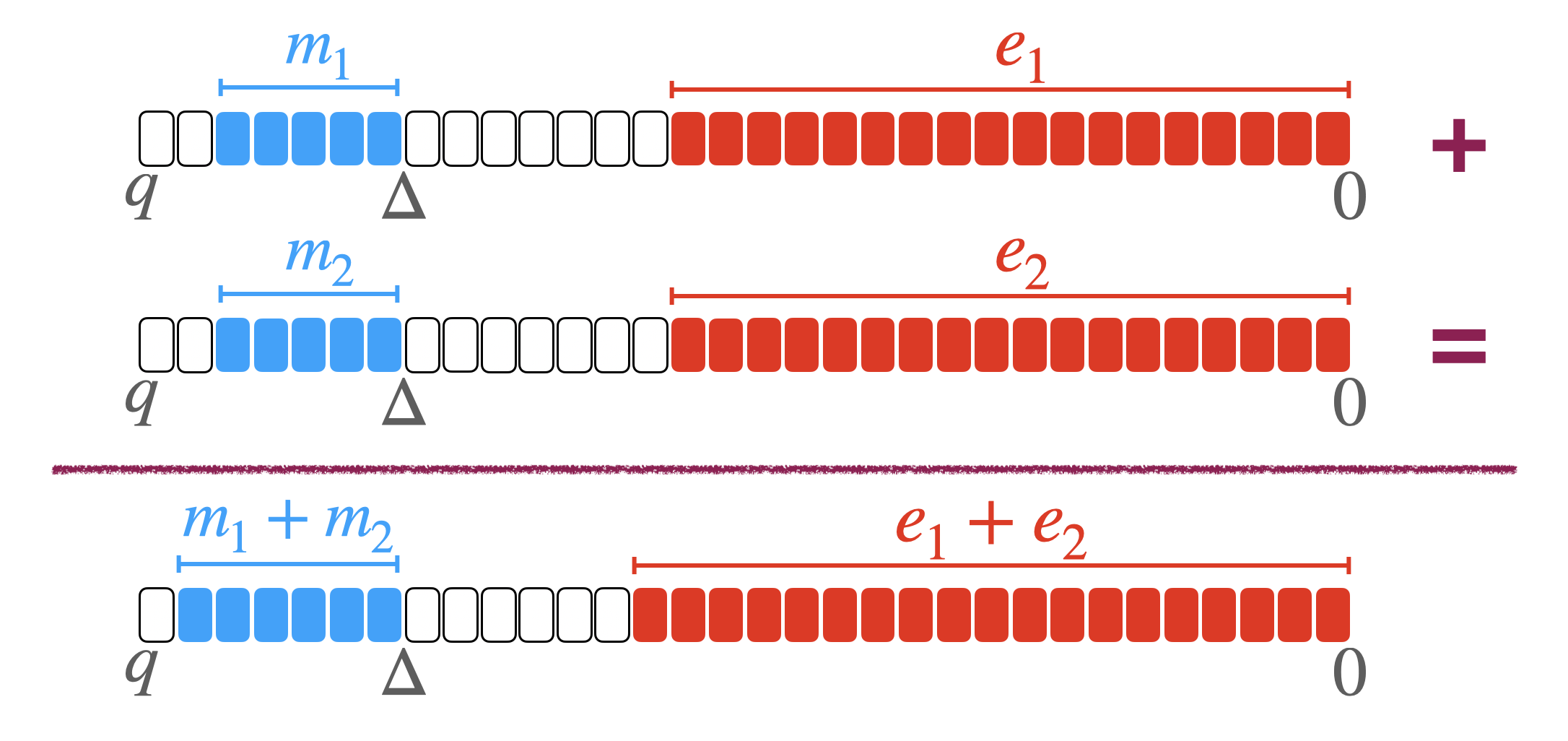
这种编码可以实现精确的分级操作。加结果就直接是加。

Encoding of binaries in GB mode.

一个带 padding 的例子是门自举(gate bootstrapping)里面的。门自举对加密 bits 的 LWE 密文计算二元门(binary gate)。实现可以看 TFHE lib 和 concrete。

编码消息是 bits，$\Delta=q/4$，所以有 1 bit 的 padding。因为自举过程中间过程要实现精确的线性组合来得到最终结果。(~~估计就是那一长串的 CMux 门~~)

Encoding of reals

固定区间内的实数，消息和错误彼此都难以分离…$m$ 占据了整个 $\mathbb{Z}_q$(~~怎么用 $\mathbb{Z}_q$ 表示实数的，计组里的表示法吗？~~)，LSB 被 $e$ 扰乱，近似(approximates)了信息。实践里，$m+e$ 和 $m\colon m\approx m+e$ 接近。但无法分辨出 $m$ 因为没有 $\Delta$ 可以区分开消息和错误(~~yysy，还是得看实数编码的方式8~~)。

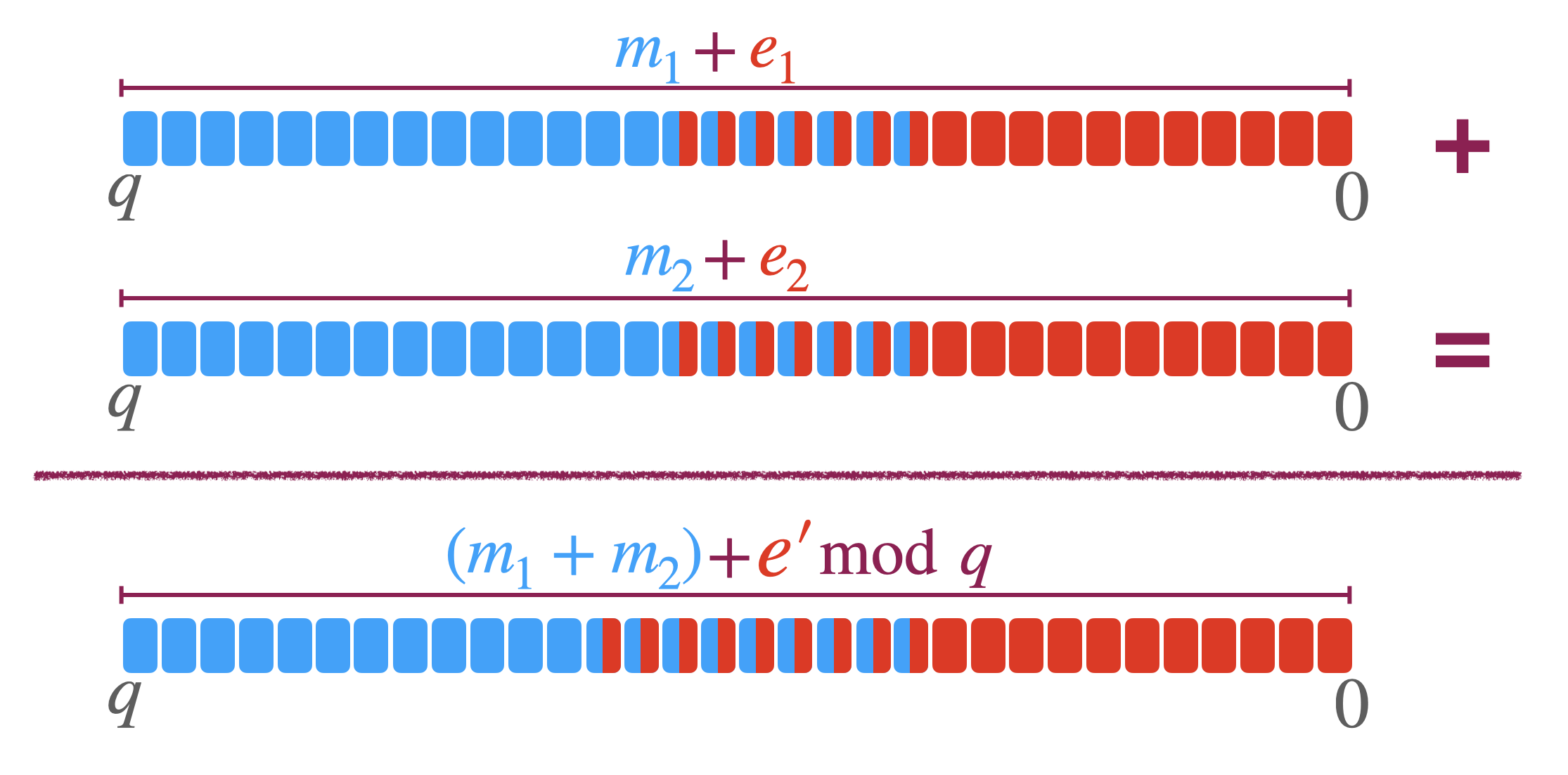
这种编码在计算近似达到特定精度的分级操作(approximate leveled operations)(加法和数乘)时很实用。

解密第二阶段 rounding 变化，在 LSB 加一个新的随机错误。可以看这篇文章。

这些编码只是一部分，还有很多。(~~感觉挺自由的~~)

Torus visualization

一维环面 $\mathbb{R}/\mathbb{Z}$ 说白了一个光滑流形，一条线，一个圆。(~~官图给的二维甜甜圈有够欺诈，想了老半天~~)(~~不知道多维环面可不可行，感觉没必要，也就用到 rounding~~)(~~说不定 ring 的 rounding 能用？~~)。

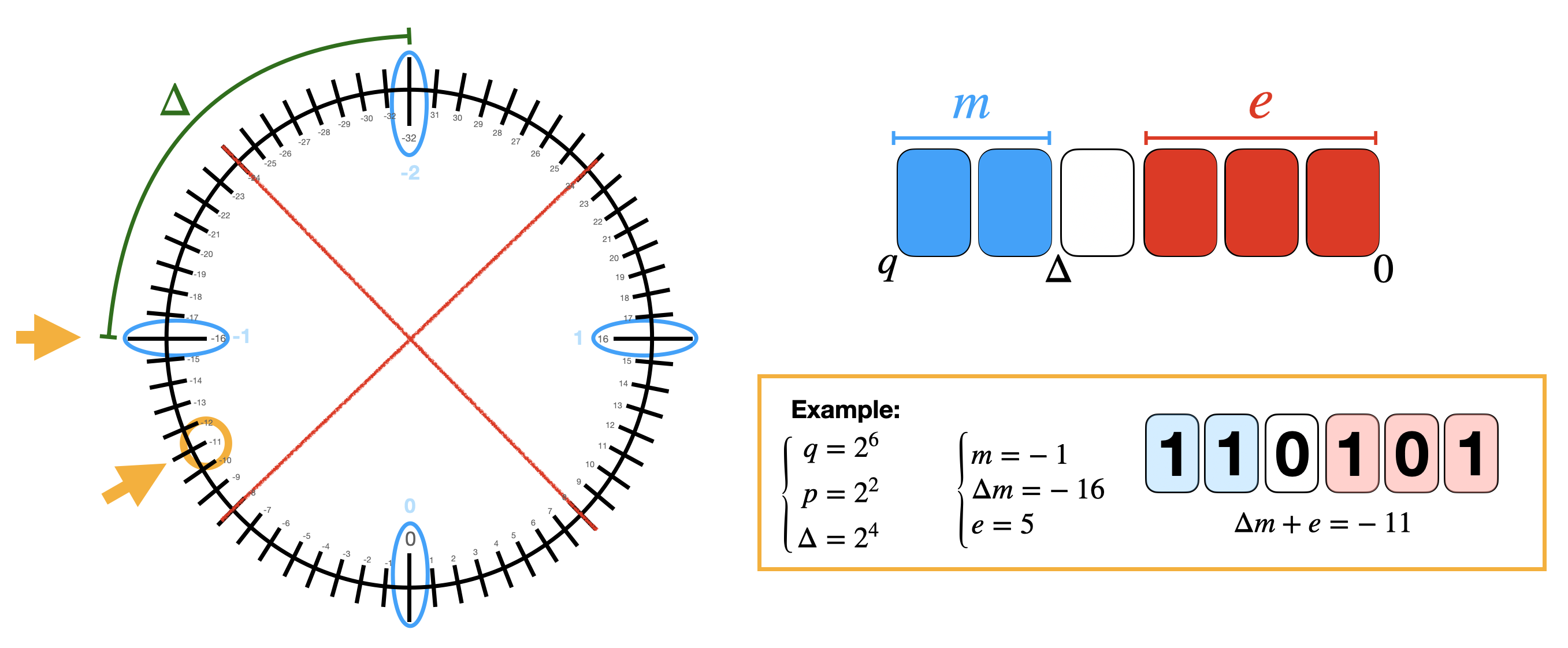
注意一下负数等价类在 torus 上的表现。

Key switching and leveled multiplications

Homomorphic multiplication by a large constant

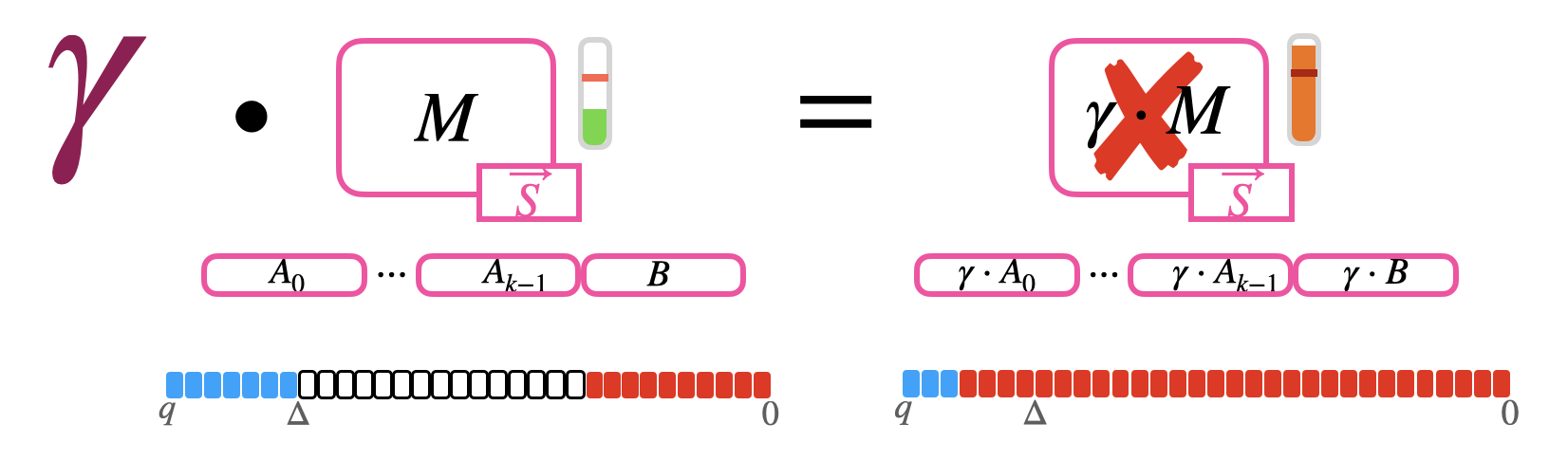
系数太大的数乘 $e$ 太大可能直接 g，所以才需要分解(decomposition)。跟 GSW 密文乘法类似。把大的常多项式分解为小的基 $\beta$：

\[\gamma=\gamma_{1} \frac{q}{\beta^{1}}+\gamma_{2} \frac{q}{\beta^{2}}+\ldots+\gamma_{\ell} \frac{q}{\beta^{\ell}}\]

分解出来的元素 $\gamma_{1},\dots,\gamma_{\ell}\in\mathbb{Z}_\beta$ ，就小了。写成 $\mathsf{Decomp}^{\beta,\ell}(\gamma)=(\gamma_{1},\dots,\gamma_{\ell})$。$q,\beta$ 一般取成 2 的幂，不然需要 rounding。

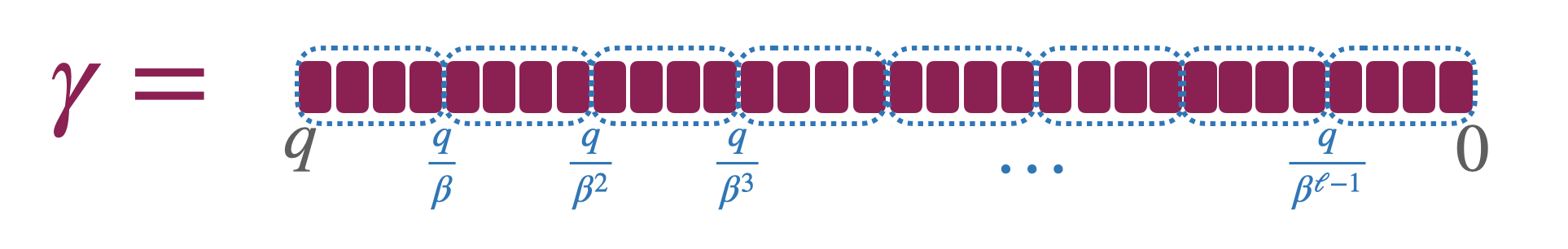
分解出来的元素都很小，现在和密文相乘对噪音影响很小。但为了得到与 $\gamma\cdot M$ 相同的结果，我们需要能逆向分解过程，重组(recompose) $\gamma$。

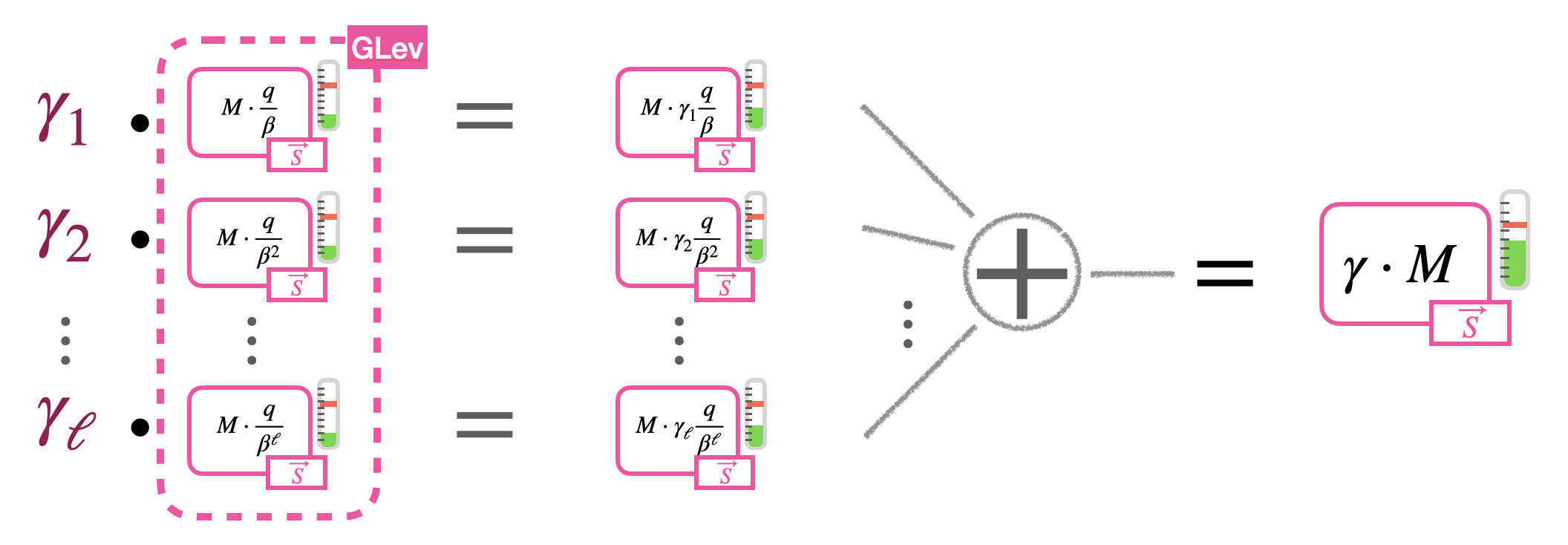
因此不将分解出来的元素与 $M$ 的 GLWE 密文相乘，而是与 $M$ 的 GLev 密文相乘。根据定义，加密了 $M$ 乘上 $\beta$ 的不同系数：

\[\bar{C}=\left(C_{1}, \dots, C_{\ell}\right) \in\left(GLWE_{\vec{S}, \sigma}\left(\frac{q}{\beta^{1}} M\right) \times \dots \times GLWE_{\vec{S}, \sigma}\left(\frac{q}{\beta^{\ell}} M\right)\right)=GLev_{\vec{S},\sigma}^{\beta,\ell}(M) \subseteq \mathcal{R}_{q}^{\ell \cdot(k+1)}\]

实践中，用一个类似内积的操作，所以将每一个分解的元素和 GLev 密文的对应元素对应相乘然后把他们加在一起。(~~所以论文里这一大堆式子是这么来的~~)

\[\left\langle \mathsf{Decomp}^{\beta,\ell}(\gamma), \overline{C} \right\rangle = \sum_{j=1}^\ell \gamma_j \cdot C_j \in GLWE_{\vec{S}, \sigma'}\left(\gamma \cdot M\right) \subseteq \mathcal{R}_q^{k+1}\]

$\sigma’$ 是噪音新方差。

输出的 GLWE 密文不再有 $\Delta$(~~因为系数加一加加乱了？~~)，新的消息可能占据整个空间 $\mathbb{Z}_q$。实践里并不直接用这个操作，而是作为更复杂操作的一个构成单元。比如密钥交换和密文之间的同态乘。

Approximate decomposition

上面的是全精度分解($\beta^\ell=q$)，有时没必要。可以近似分解到指定精度($\beta^\ell<q$)。分解之前对 LSB 进行 rounding。

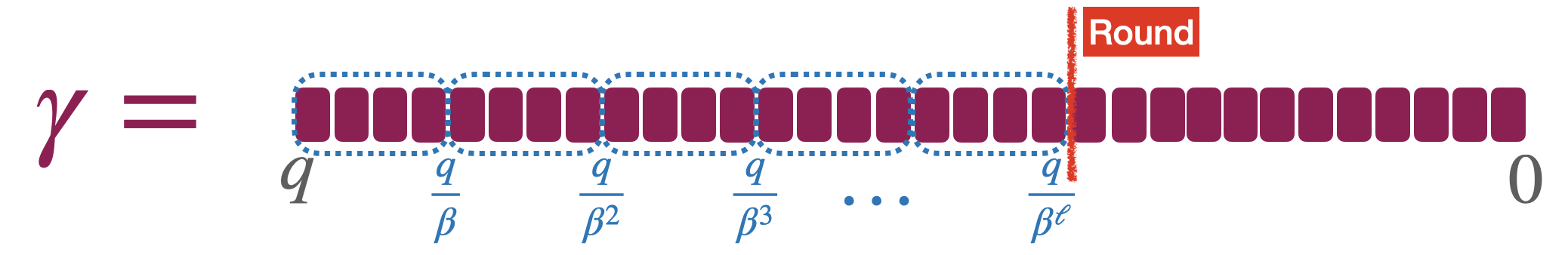
分解参数选的恰当就不会影响到计算正确性。LSB 肯定是噪音。一些同态操作里非常方便。

Multiplication by a large polynomial

同样的方法乘上一个大的多项式。分解多项式再与 GLev 密文内积。假设多项式是 $\Lambda = \sum_{i=0}^{N-1} \Lambda_i \cdot X^i$，分解就是

\[\mathsf{Decomp}^{\beta,\ell}(\Lambda) = (\Lambda^{(1)}, \ldots, \Lambda^{(\ell)})\]

$\Lambda^{(j)} = \sum_{i=0}^{N-1} \Lambda_{i,j} \cdot X^i$，其中 $\Lambda_{i,j} \in \mathbb{Z}_\beta$ 使得：

\[\Lambda = \Lambda^{(1)} \frac{q}{\beta^1} + \ldots + \Lambda^{(\ell)} \frac{q}{\beta^\ell}.\]

如果分解是近似的，等式也是近似的。这个操作是密钥交换和同态乘法的主要构成单元。

Toy example

老参数：$q=64,p=4,\Delta = q/p = 16,N=4,k = 2$，随机多项式：

\[\Lambda = \Lambda_0 + \Lambda_1 X + \Lambda_2 X^2 + \Lambda_3 X^3 = 28 - 5 X - 30 X^2 + 17 X^3\]

选定 $\beta=4,\ell=2,\beta^\ell=16$ ，表示对 4 个 MSB 进行分解。分解之前先对所有参数 rounding。先写成二进制表示：(~~补码。成计组复习了(悲)~~)

$\Lambda_0 = 28 \longmapsto (0, 1, 1, 1 {\color{red} \mid} 0, 0)$ after rounding: $\Lambda’_0 \longmapsto (0, 1, 1, 1);$

$\Lambda_1 = -5 \longmapsto (1, 1, 1, 0 {\color{red} \mid} 1, 1)$ after rounding: $\Lambda’_1 \longmapsto (1, 1, 1, 1);$

$\beta=4$ 两位两位拆出来，分别映射到 $\qty{-2,-1,0,1}$ (~~带正负~~)取值，最后拆出来

\[\begin{cases} \Lambda^{(1)} = -2 -2 X^2 + X^3 \\ \Lambda^{(2)} = -1 - X + X^2 \\ \end{cases}\]

$\Lambda_2$ 由靠近低位的组成。最终可以逆向生成 $\Lambda$：

\[\Lambda^{(1)} \cdot \frac{q}{\beta^1} + \Lambda^{(2)} \cdot \frac{q}{\beta^2} = (-2 -2 X^2 + X^3) \cdot 16 + (-1 - X + X^2) \cdot 4 = 28 - 4 X - 28 X^2 + 16 X^3 \in \mathcal{R}_q\]

Key switching

密文实际上就是一个大的常向量、多项式，多项式向量，由模 $q$ 整数组成，(伪)均匀随机。

密钥更换的常规操作就是用原来的密钥解密，再用新的密钥加密。但需要全同态的操作。并非直接将密钥提供，而是提供原密钥 $\vec{S}$ 在新的密钥 $\vec{S}’$ 下的密文。

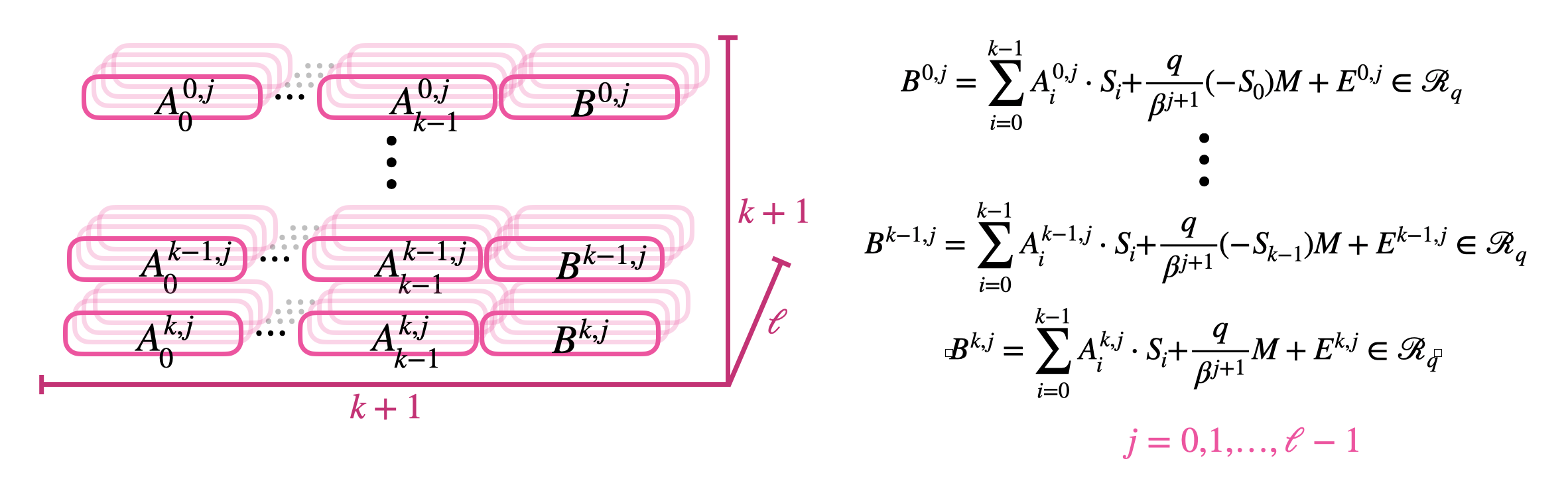
这里就要用到大的常数和密文之间的乘法，密文就是 $S_i$ 的GLev 密文，大常数是 $A_i$。

所以密钥更换密钥就是由 $\vec{S}$ 的每个元素 $S_i$ 在新的密钥 $\vec{S}’$ 下的 GLev 密文组成：

\[\mathsf{KSK}_i \in \left( GLWE_{\vec{S}', \sigma_{\mathsf{KSK}}}\left(\frac{q}{\beta^1} S_i\right) \times \ldots \times GLWE_{\vec{S}', \sigma_{\mathsf{KSK}}}\left(\frac{q}{\beta^\ell} S_i\right) \right) = GLev^{\beta, \ell}_{\vec{S}', \sigma_{\mathsf{KSK}}}(S_i) \subseteq \mathcal{R}_q^{\ell \cdot (k+1)}.\]

实践中，密钥更换就这样：

\[C' = \underbrace{\overbrace{(0, \ldots, 0, B)}^{\text{Trivial GLWE of } B} - \sum_{i=0}^{k-1} \overbrace{ \langle \mathsf{Decomp}^{\beta,\ell}(A_i), \mathsf{KSK}_i \rangle}^{\text{GLWE encryption of } A_i S_i} }_{\text{GLWE encryption of } B - \sum_{i=0}^{k-1} A_i S_i = \Delta M + E}\in GLWE_{\vec{S}', \sigma'}(\Delta M) \subseteq \mathcal{R}_q^{k+1}.\]

密钥从 $\vec{S}$ 更换到 $\vec{S}’$ 但是密文保持不变。

和 GLWE 密文的全同态计算(~~bootstrapping~~)第一步相似(~~都是解密~~)，只是不进行第二步(~~rounding~~)。这样并不会降低噪音，相反，会增大。

Various types of key switching

one LWE to one LWE,
one RLWE to one RLWE,
one LWE to one RLWE, putting the message encrypted in the LWE into one of the coefficients of the RLWE ciphertext,
many LWE to one RLWE, packing the messages encrypted in the many LWE inputs into the RLWE ciphertext.

Other uses of the key switching

可以调参数。$\vec{S}’$ 的 $N,k$ 可以和输入的不一样。用的很多，比如 bootstrapping。

External product

大常数乘上密文需要先将大常数分解，然后再和 GLev 密文进行重组得到数乘结果，GLWE 密文由一连串的大常数组成，结合一下：

跟密钥更换类似，对于两个密文，拎一个出来当成要被分解的 GLWE 密文，另外一个是一串 GLev 密文。和密钥更换的不同点是，密钥交换只把 mask 拎出来，这次是 mask 和 body 都要。

GGSW 正好满足要求(~~一连串的 GLev 密文~~)。所以输入一个 GLWE，一个 GGSW，输出一个 GLWE 密文加密了两个消息的乘积。

一个 GLWE 密文加密了消息 $M_1\in\mathcal{R}_q$，密钥是 $\vec{S} = (S_0, \ldots, S_{k-1}) \in \mathcal{R}^k$：
\[C = (A_0, \ldots, A_{k-1}, B) \in GLWE_{\vec{S}, \sigma}(\Delta M_1) \subseteq \mathcal{R}_q^{k+1}\]
一个 GGSW 密文加密了消息 $M_2\in\mathcal{R}_q$，密钥同样是 $\vec{S} = (S_0, \ldots, S_{k-1}) \in \mathcal{R}^k$：
\[\overline{\overline{C}} = (\overline{C}_0, \ldots, \overline{C}_{k-1}, \overline{C}_k) \in GGSW^{\beta, \ell}_{\vec{S}, \sigma}(M_2) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}\]
其中 $\overline{C}_i \in GLev^{\beta, \ell}_{\vec{S}, \sigma}(-S_i M_2)$，$i \in [0..k-1]$ 且 $\overline{C}_k \in GLev^{\beta, \ell}_{\vec{S}, \sigma}(M_2)$

则外积运算 $\boxdot$ 如下：

\[\begin{aligned} C' &= \overline{\overline{C}} \boxdot C = \langle \mathsf{Decomp}^{\beta,\ell}(C), \overline{\overline{C}} \rangle \\ &= \underbrace{ \overbrace{\langle \mathsf{Decomp}^{\beta,\ell}(B), \overline{C}_k \rangle}^{\text{GLWE encrypt. of } B M_2} + \sum_{i=0}^{k-1} \overbrace{\langle \mathsf{Decomp}^{\beta,\ell}(A_i), \overline{C}_i \rangle}^{\text{GLWE encrypt. of } - A_i S_i M_2} }_{\text{GLWE encrypt. of } B M_2 - \sum_{i=0}^{k-1} A_i S_i M_2 \approx \Delta M_1 M_2} \in GLWE_{\vec{S}, \sigma^{\prime\prime}}(\Delta M_1 M_2) \subseteq \mathcal{R}_q^{k+1} \end{aligned}\]

输出的 GLWE 噪音比输入的 GLWE 大，记作 $\sigma^{\prime\prime}$。

External Product vs. Key Switching

外积就像是用了额外元素的密钥交换密钥(算 $BM_2$ GLWE 密文時的 $\overline{C}_k$ 的 GLev 密文)的密钥交换。

外积就像是不交换密钥的密钥交换。在 GGSW 密文里用来加密的密钥和 GLev 密文里的是同一个密钥。对比 $GLev^{\beta, \ell}_{\vec{S}’, \sigma_{\mathsf{KSK}}}(S_i)$ 和 $\overline{C}_i \in GLev^{\beta, \ell}_{\vec{S}, \sigma}(-S_i M_2)$

用了不同的密钥加密 $\vec{S}’$ 的 GGSW 密文里面是相同的密钥 $\vec{S}$ 的 GLWE 密文的外积如 $GLev^{\beta, \ell}_{\vec{S}’, \sigma_{\mathsf{KSK}}}(S_i)$ 叫做功能性密钥更换(functional key switching)。实际上它运行了一个函数(乘上加密的常数)同时更换了密钥。

Internal product

外积叫外积因为需要一个外部的 GGSW 密文运作(记法跟模运算的数乘一致，$\mathbb{T}_N\bqty{X}\bmod(X^N+1)$ 和 $\mathcal{R}_q$ 的运算)。没有 GLWE 之间的内积，或者说没有直接的方法。B/FV GLWE 密文之间的内积是通过类似密钥更换的方式实现的。

GGSW 有内积。GGSW 是一串 GLev 密文，GLev 密文是一串 GLWE 密文。三段论 GGSW 密文是一串 GLWE 密文。外积在 GLWE 跟 GGSW 之间定义，我们可以定义内积为一连串的外积，拎一个 GGSW 密文出来把它看成一系列的 GLWE 密文，跟另一个 GGSW 进行外积。所有输出的 GLWE 密文组成了 GGSW 密文。所以输入：

一个 GGSW 密文加密了消息 $M_1\in\mathcal{R}_q$，密钥是 $\vec{S} = (S_0, \ldots, S_{k-1}) \in \mathcal{R}^k$：
\[\overline{\overline{C}}_1 = (\overline{C}_0, \ldots, \overline{C}_{k-1}, \overline{C}_k) \in GGSW^{\beta, \ell}_{\vec{S}, \sigma}(M_1) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}\]
其中，对于 $i \in [0..k-1]$：
\[\overline{C}_i = (C_{i,1}, \ldots, C_{i,\ell}) \in GLev^{\beta, \ell}_{\vec{S}, \sigma}(-S_i M_1) \subseteq \mathcal{R}_q^{\ell \cdot (k+1)}\]
包含 $C_{i,j} \in GLWE_{\vec{S}, \sigma}\left(\frac{q}{\beta^j} (-S_i M_1) \right)$，对于 $j \in [1..\ell]$，且：
\[\overline{C}_k \in (C_{k,1}, \ldots, C_{k,\ell}) \in GLev^{\beta, \ell}_{\vec{S}, \sigma}(M_1) \subseteq \mathcal{R}_q^{\ell \cdot (k+1)}\]
包含 $C_{k,j} \in GLWE_{\vec{S}, \sigma}\left(\frac{q}{\beta^j} M_1 \right)$，对于 $j \in [1..\ell]$。
一个 GGSW 密文加密了消息 $M_2\in\mathcal{R}_q$，密钥同样是 $\vec{S} = (S_0, \ldots, S_{k-1}) \in \mathcal{R}^k$：

\[\overline{\overline{C}}_2 \in GGSW^{\beta, \ell}_{\vec{S}, \sigma}(M_2) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}\]

则内积运算 $\boxtimes$ 如下：

\[\overline{\overline{C}}' = \overline{\overline{C}}_2 \boxtimes \overline{\overline{C}}_1 = (\overline{\overline{C}}_2 \boxdot C_{0,1}, \ldots, \overline{\overline{C}}_2 \boxdot C_{0,\ell}, \ldots, \overline{\overline{C}}_2 \boxdot C_{k,1}, \ldots, \overline{\overline{C}}_2 \boxdot C_{k,\ell})\]

可以发现：

\[\left\lbrace \begin{aligned} \overline{\overline{C}}_2 \boxdot C_{i,j} &\in GLWE_{\vec{S}, \sigma^{\prime\prime}}\left( \frac{q}{\beta^j} (-S_i M_1 M_2) \right) &\text{for } i \in [0..k-1], j \in [1..\ell] \\ \overline{\overline{C}}_2 \boxdot C_{k,j} &\in GLWE_{\vec{S}, \sigma^{\prime\prime}}\left( \frac{q}{\beta^j} (M_1 M_2) \right) &\text{for } j \in [1..\ell] \end{aligned} \right.\]

综上所述：

\[\overline{\overline{C}}' = \overline{\overline{C}}_2 \boxtimes \overline{\overline{C}}_1 \in GGSW^{\beta, \ell}_{\vec{S}, \sigma^{\prime\prime}}(M_1 M_2) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}.\]

噪音会变大，记作 $\sigma^{\prime\prime}$(跟外积一样)。

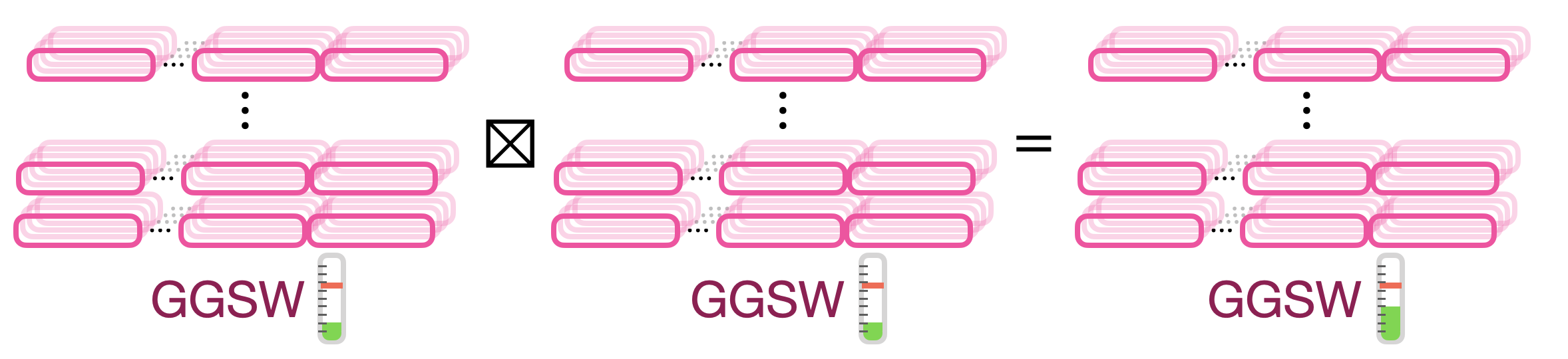
Internal Product vs. External Product

外积算得快但不是可组合的(composable)。内积的输出可以作为任一个输入，但外积的输出(GLWE 密文)只能用作一个输入，还得在拎一个 GGSW 过来。

TFHE 提出了一种同态构造 GGSW 密文的方法，叫电路自举(circuit bootstrapping)，可以看这个。

TFHE 主要用外积，尽量避免使用内积。

CMux

没啥好说的，直接两张图：

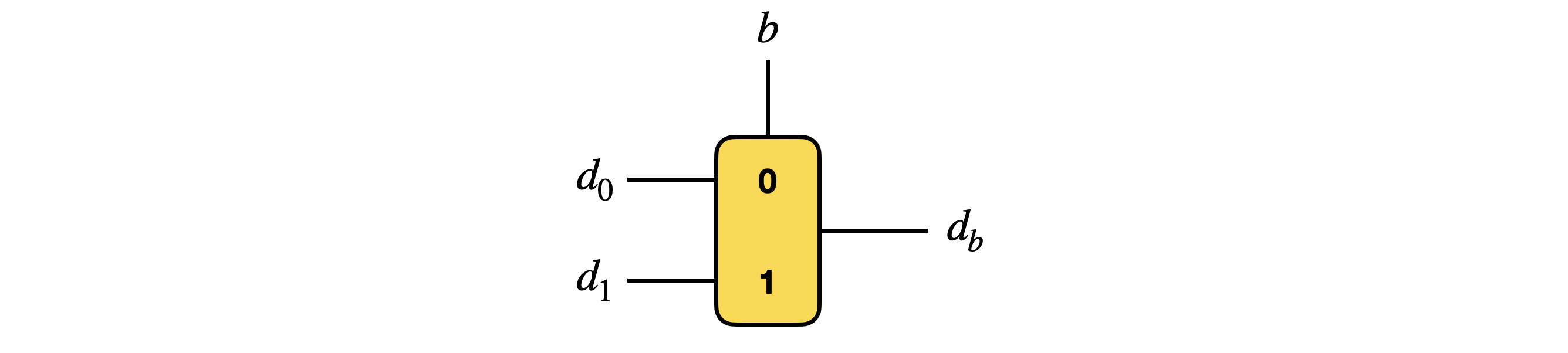
输入 $b$ GGSW 密文，$d_0,d_1$ GLWE 密文，外积，同态加减，输出 $d_b$ GLWE 密文。

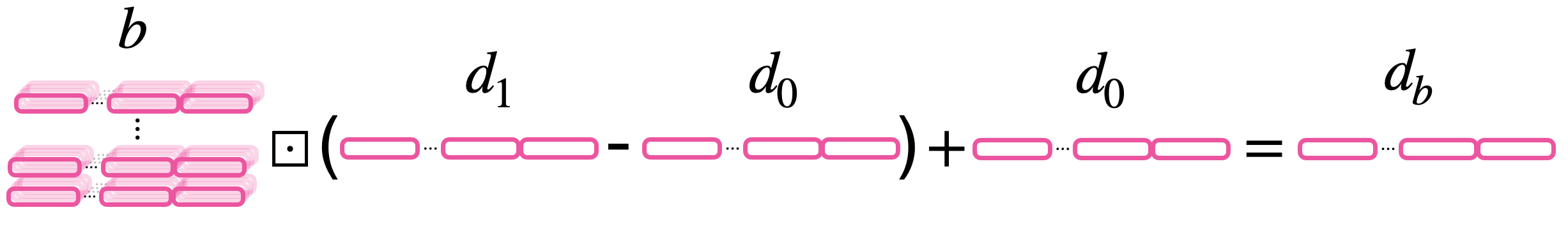
Modulus Switching

换模数。TFHE 里面一般用在 LWE 密文，也可以拓展到 GLWE 密文。

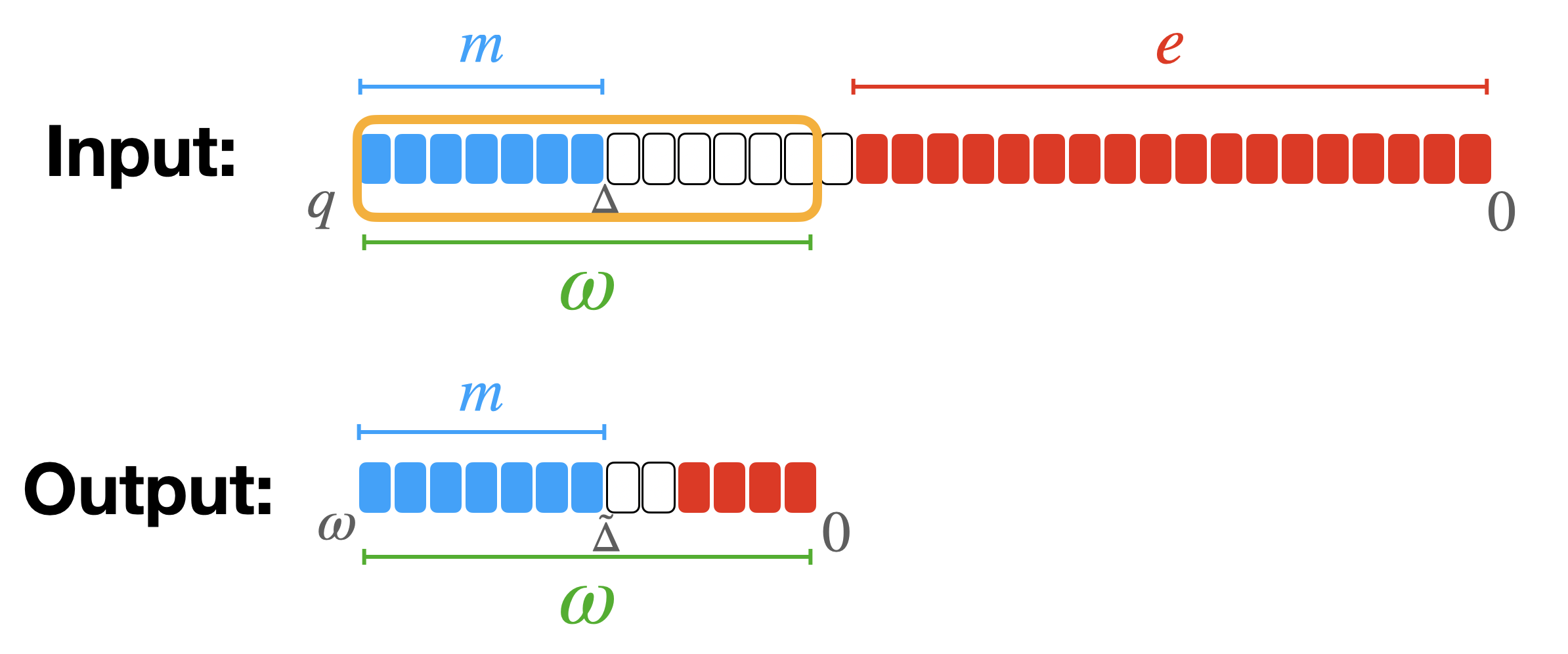
比如正整数 $\omega$，将 LWE 密文的所有部件的模数从 $q$ 更换到 $\omega$：

\[\tilde{a}_i = \left\lfloor \frac{\omega \cdot a_i}{q} \right\rceil \in \mathbb{Z}_\omega.\]

所以结果是一个新密文：

\[\tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{a}_n = \tilde{b}) \in LWE_{\vec{s}, \sigma}(\tilde{\Delta} m) \subseteq \mathbb{Z}_\omega^{n+1}.\]

一般换到更小的 $\omega$，且都是 2 的幂，$p < \omega < q$，所以 $\Delta$ 相应变为 $\tilde{\Delta} = \frac{\omega \cdot \Delta}{q} = \omega/p$。如果不是 2 的幂需要 rounding。

操作形象描述为保留原密文的 $\log_2(\omega)$ MSB，也就是消息编码的地方，这么做噪音会变大很多，i.e.，离消息编码的位置更近(~~$\Delta$ 变小了~~)。小心使用。

Sample Extraction

将 GLWE 多项式密文的一个系数(对应明文多项式的一个系数)拎出来作为一个 LWE 密文。

不增加噪音，只是简单的复制 GLWE 密文的一些系数输出 LWE 密文。

对于 GLWE 密文加密了 $M = \sum_{j=0}^{N-1} m_j X^j \in \mathcal{R}_p$，密钥是 $\vec{S} = (S_0 = \sum_{j=0}^{N-1} s_{0,j} X^j, \ldots, S_{k-1} = \sum_{j=0}^{N-1} s_{k-1,j} X^j) \in \mathcal{R}^k$，是一个 $k+1$ 元组：

\[C = \left(A_0 = \sum_{j=0}^{N-1} a_{0,j} X^j, \ldots, A_{k-1} = \sum_{j=0}^{N-1} a_{k-1,j} X^j, B = \sum_{j=0}^{N-1} b_j X^j \right) \in GLWE_{\vec{S}, \sigma}(\Delta M) \subseteq \mathcal{R}_q^{k+1}\]

如果想要提取消息 $M$ 的第 $h$ 个系数，$0 \leq h < N$，LWE 密文 $n = k N$，且密钥为提取的密钥 $\vec{s}$，为 GLWE 密钥的系数复制。

\[\vec{s} = (s_{0,0}, \ldots, s_{0,N-1}, \ldots, s_{k-1,0}, \ldots, s_{k-1,N-1}) \in \mathbb{Z}^{kN}\]

之后通过简单复制一些 GLWE 密文的系数构建 LWE 密文 $c = (a_0, \ldots, a_{n-1}, b) \in \mathbb{Z}^{n+1}_q$：

\[\begin{cases} a_{N\cdot i + j} \leftarrow a_{i,h-j} &\text{ for } 0 \leq i < k, 0 \leq j \leq h \\ a_{N\cdot i + j} \leftarrow - a_{i,h-j+N} &\text{ for } 0 \leq i < k, h+1 \leq j < N \\ b \leftarrow b_h & \\ \end{cases}\]

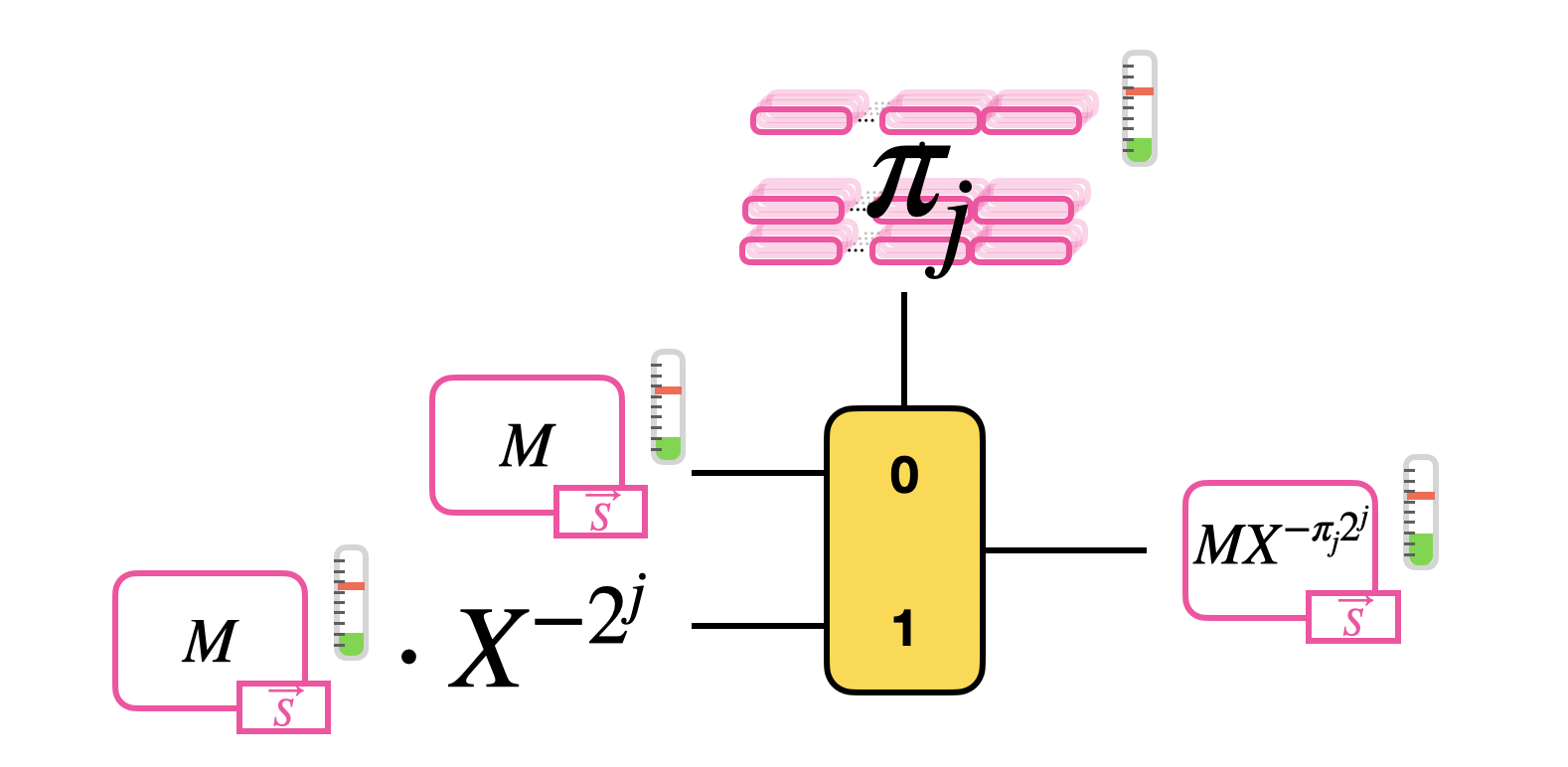
把「禁則事項」多项式第「禁則事項」项多项式系数转到常数项。

因为位置 $0 \leq \pi < N$ 是一个整数，Cmux 选择端输入是一个 bit，首先将其二进制表示：

\[\pi = \pi_0 + \pi_1 \cdot 2 + \pi_2 \cdot 2^2 + \ldots + \pi_\delta \cdot 2^\delta\]

其中 $\delta = \log_2(N)$，我们想算的是：

\[\begin{aligned} M \cdot X^{-\pi} &= M \cdot X^{-\pi_0 -\pi_1 \cdot 2 -\pi_2 \cdot 2^2 + \ldots -\pi_\delta \cdot 2^\delta} \\ &= M \cdot X^{-\pi_0} \cdot X^{-\pi_1 \cdot 2} \cdot X^{-\pi_2 \cdot 2^2} \cdot \ldots \cdot X^{-\pi_\delta \cdot 2^\delta}. \\ \end{aligned}\]

拎一个 $X^{-\pi_j \cdot 2^j}$ 出来，因为 $\pi_j$ 是 bit，算这玩意只有两种情况：

\[M \cdot X^{-\pi_j \cdot 2^j} = \begin{cases} M &\text{ if } \pi_j = 0 \\ M \cdot X^{-2^j} &\text{ if } \pi_j = 1 \\ \end{cases}\]

用一个 CMux 实现：

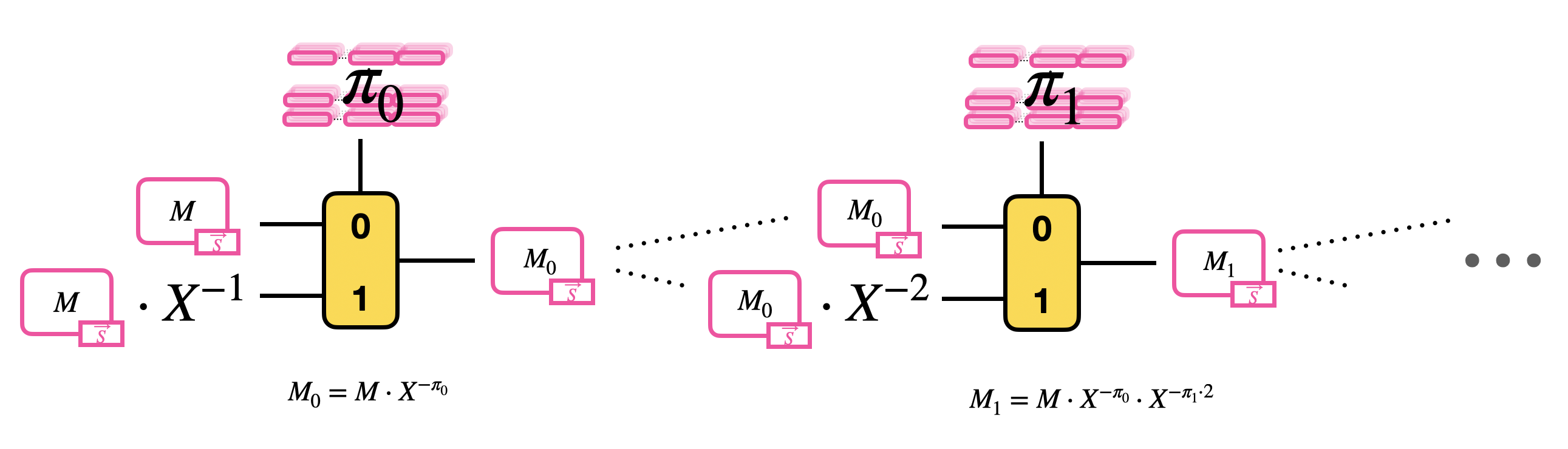
递归的计算所有多项式项，所以表现为 $\delta$ 个 CMux 串联。

Bootstrapping

减小噪音的方法是同态解密，解密是唯一可以取消一切随机性的操作。TFHE 的自举在 LWE 密文上进行，所以 $c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1}$ 加密了消息 $m \in \mathbb{Z}_p$，密钥是 $\vec{s} = (s_0, \ldots, s_{n-1}) \in \mathbb{Z}^n$。解密分为两步：

算 $b-\sum_{i=0}^{n-1} a_i s_i = \Delta m + e \in \mathbb{Z}_q$
去掉 $\Delta$ 并取整 $\left\lfloor \frac{\Delta m + e}{\Delta} \right\rceil = m$

TFHE 通过将(负的) $b-\sum_{i=0}^{n-1} a_i s_i = \Delta m + e$ 的计算放在单项式 $X$ 的指数里面，然后用它对查找表(LUT)进行旋转，进行解密的第二步。从第二步开始。

Step 2

将 $\Delta m + e$ 处理为 $m$，需要将这两者联系起来。$\Delta m + e\in\mathbb{Z}_q,m\in\mathbb{p},p<q$，所以我们需要重复 $m$ 做成一个 LUT，将所有 $\Delta m + e$ 都取整为 $m$。冗余的框框叫做 mega-cases。

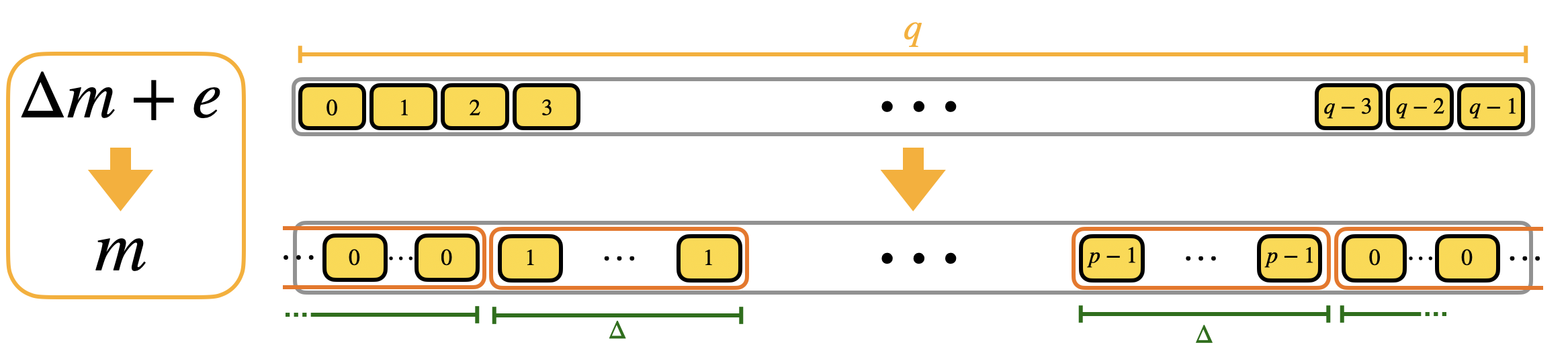
通过多项式旋转对这个查找表进行查找。将这个冗余查找表的所有元素作为一个多项式的所有系数，然后通过同态的乘 $X^{-(\Delta m + e)}$ 将这个多项式旋转到 $\Delta m + e$ 位置，最终将一个元素转到常数项，其所在的 mega-case 就是 $m$ 的值。所以我们想读多项式的某一项时对其进行旋转将待读系数放到常数项而不是直接去找系数所在位置。(快？)

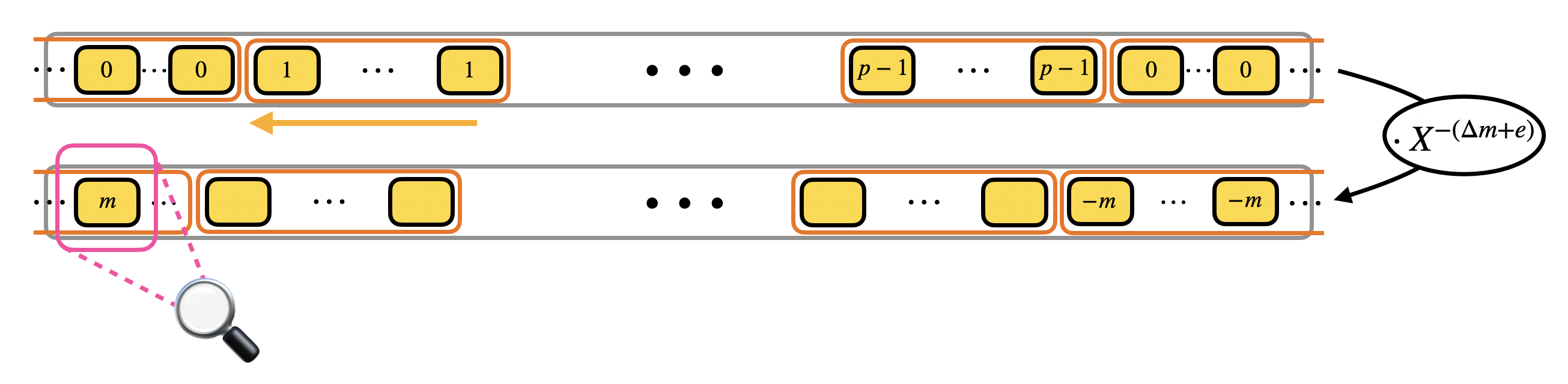
然而 TFHE 的多项式都是模多项式 $X^N + 1$ 的多项式，所以最多有 $N$ 个系数，一般 $N=2^{10},q=2^{32}$ 不足以放下整个查找表的 $q$ 个元素，所以用前面提到的 modulus switching 压缩信息。

模 $X^N + 1$ 单项式 $X$ 的阶是 $2N$ ($X^N \equiv -1,X^{2N} \equiv 1$)，也就是说确定了多项式的 $N$ 个系数，我们实际上确定了 $2N$ 个系数。另一半是负的。这个属性叫做 negacyclic property。如果要同态计算的 LUT 是 negacyclic 的，你可以编码所有 $m$ 可能的 $p$ 个取值，也可以只编码 $\frac{p}{2}$。所以如果使用的不是 negacyclic LUT，需要在消息编码的时候添加额外的 1 bit padding。modulus switching 从 $q$ 到 $2N$。(~~采用 negacyclic 应该降低了消息编码长度，为了兼容才加了 padding 和确定为 2N~~)

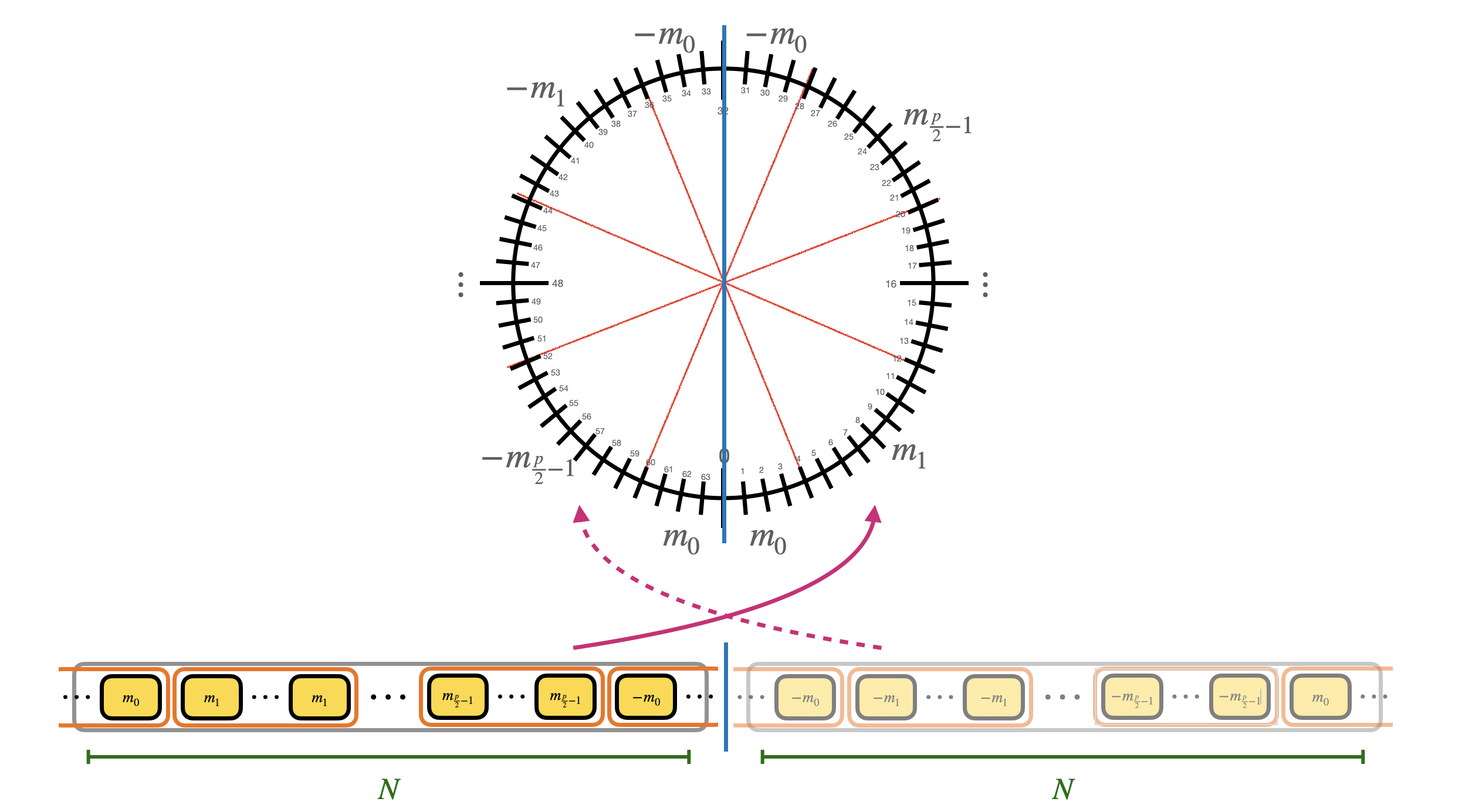
Step 1

同态计算 $X^{-(\Delta m + e)}$。modulus switching 从 $q$ 到 $2N$：

\[c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1} \longmapsto \tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{b}) \in LWE_{\vec{s}, \sigma'}(\tilde{\Delta} m) \subseteq \mathbb{Z}_{2N}^{n+1}\]

之后用盲转把 modulus switching 的输出放到 $X$ 的指数上。这个过程输入一个 LUT 多项式的平凡 GLWE 加密，记作 $V$，$\tilde{c} = (\tilde{a}0, \ldots, \tilde{a}{n-1}, \tilde{b})$ 的所有元素，和 LWE 密钥元素 $\vec{s} = (s_0, \ldots, s_{n-1})$ 在新的 GGSW 密钥 $\vec{S}’$ 下的加密(~~key switching~~)。这个 GGSW 加密密钥的密文就是自举密钥。步骤如下：

初始化。$V\cdot X^{-\tilde{b}}$ (rotation)。
将平凡 GLWE 密文 $V\cdot X^{-\tilde{b}} = V_0$ 作为第一个 CMux 的输入。判断端输入是 LWE 密钥元素 bit $s_0$ 的 GGSW 加密；0,1 分别对应 $V_0$ 和 $V_0 \cdot X^{\tilde{a}_0}$。等同于输出 GLWE 密文的 $V_1 = V_0 \cdot X^{\tilde{a}_0 s_0}$
将 GLWE 密文 $V_1$ 作为第二个 CMux 的输入。判断端输入是 LWE 密钥元素 bit $s_1$ 的 GGSW 加密；0,1 分别对应 $V_1$ 和 $V_1 \cdot X^{\tilde{a}_1}$。等同于输出 GLWE 密文的 $V_1 = V_0 \cdot X^{\tilde{a}_0 s_0}$。循环全部的 $n$ 个 CMux。

盲转的最终结果是 GLWE 密文：

\[\begin{aligned} V_n &= V_{n-1} \cdot X^{\tilde{a}_{n-1} s_{n-1}} \\ &= \ldots \\ &= V \cdot X^{-\tilde{b}} \cdot X^{\tilde{a}_0 s_0} \cdot \ldots \cdot X^{\tilde{a}_{n-1} s_{n-1}} \\ &= V \cdot X^{-\tilde{b} + \sum_{i=0}^{n-1} \tilde{a}_i s_i} = V \cdot X^{-(\tilde{\Delta} m + \tilde{e})} \\ \end{aligned}\]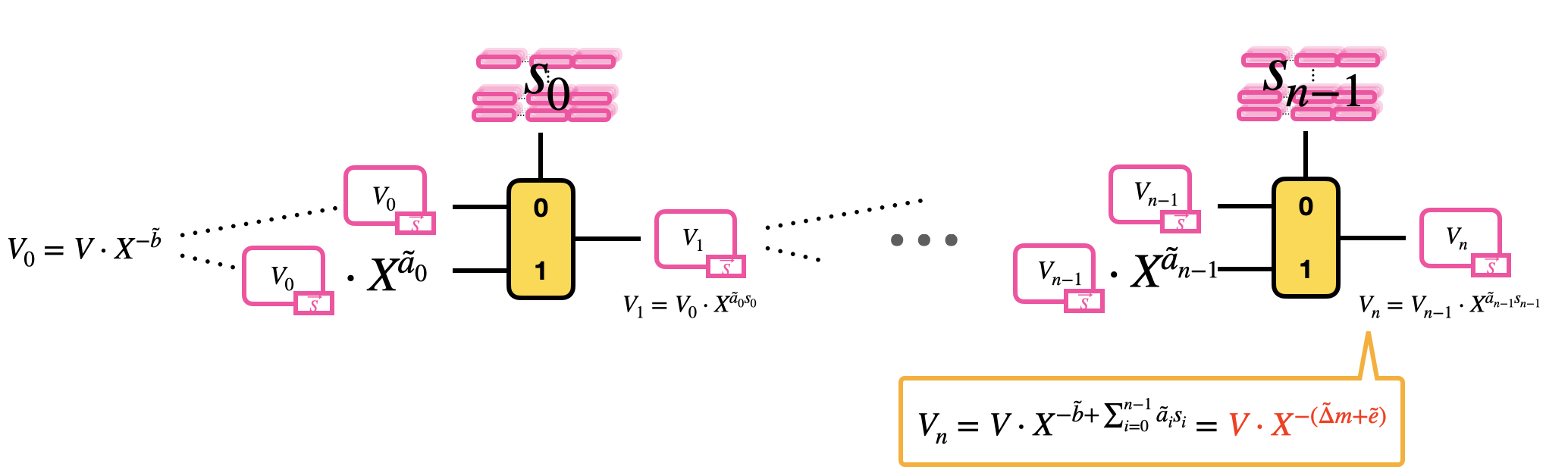

Putting Things Together

最后一步是 sample extraction。盲转的结果 $V \cdot X^{-(\tilde{\Delta} m + \tilde{e})}$ 是一个多项式，其常数项对应 $m$ 的 mega-case 的一个元素。用 sample extraction 给常数项提取出来作为 LWE 密文。一些高级用法：

盲转实际上计算了一个编码在多项式 $V$ 里面的 LUT。前面只说了是自举的输出是一个 $m$ 的密文，并且我们将 $m$ 编码到了 $V$ 里面，但 LUT 能编码输入值的任何函数。所以我们用 $f_m$ 替代 $m$ 输入 $V$ 中，同时降低了噪音。所以叫 programmable bootstrapping。$m$ 实际上就是 $f_m$ 的特殊情况。不管 $f_m$ 的值是啥通常在前面加个标量，可以是 $\Delta$ 也可以是新的 $\Delta’$。执行函数只是输入了不同的函数值不会增加开销。
多项式 $V$ 通常明文给出(输入给自举一个 $V$ 的平凡加密)。如果我们想保密要计算的 LUT，可以扔给自举一个非平凡加密的 $V$ 的 GLWE 密文。对噪音有极小的影响。因此隐藏要计算的函数对性能几乎没有影响。
虽然自举可以消除噪音，但自举执行过程的一大堆同态操作又会使噪音增长。因此自举密钥选取过程中需要选择尽可能小的参数(在保持安全等级的情况下)。因此使得输出的噪音要比输入的 LWE 密文小。因此错误的参数选择是致命的，并且是 TFHE 最难的部分之一。

总结一下。自举输入一个 LWE 密文 $c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1}$，一个多项式 $V \in \mathcal{R}_q$ 和一个自举密钥 $\mathsf{BK} = (\mathsf{BK}_0, \ldots, \mathsf{BK}_{n-1})$，其中 $\mathsf{BK}_i \in GGSW^{\beta, \ell}_{\vec{S}’, \sigma}(s_i) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}$ 是 LWE 密钥的每一个 bit $s_i$ 在 GLWE 密钥 $\vec{S}’$ 下的 GGSW 加密。步骤如下：

Modulus switching: 输入 LWE 密文 $c$ 从 $q$ 到 $2N$ 换模，输出：

\[\tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{b}) \in LWE_{\vec{s}, \sigma'}(\tilde{\Delta} m) \subseteq \mathbb{Z}_{2N}^{n+1}\]

Blind rotation: 用 modulus switching 输出的 LWE 密文 $\tilde{c}$ 和自举密钥 $\mathsf{BK}$ 对多项式 $V$ (平凡加密的 GLWE 密文) 盲转，输出一个 GLWE 密钥 $\vec{S}’$ 下 $V \cdot X^{-(\tilde{\Delta} m + \tilde{e})}$ 的 GLWE 密文。
Sample extraction: 提取盲转输出 GLWE 密文的常数项，作为 $f_m$ 的 LWE 密文，密钥是提取的 LWE 密钥 $\vec{s}’$。

如果想将输出的 LWE 密文的密钥 $\vec{s}’$ 转换为输入的 $\vec{s}$，可以用 LWE-to-LWE 密钥更换。总结如下图：

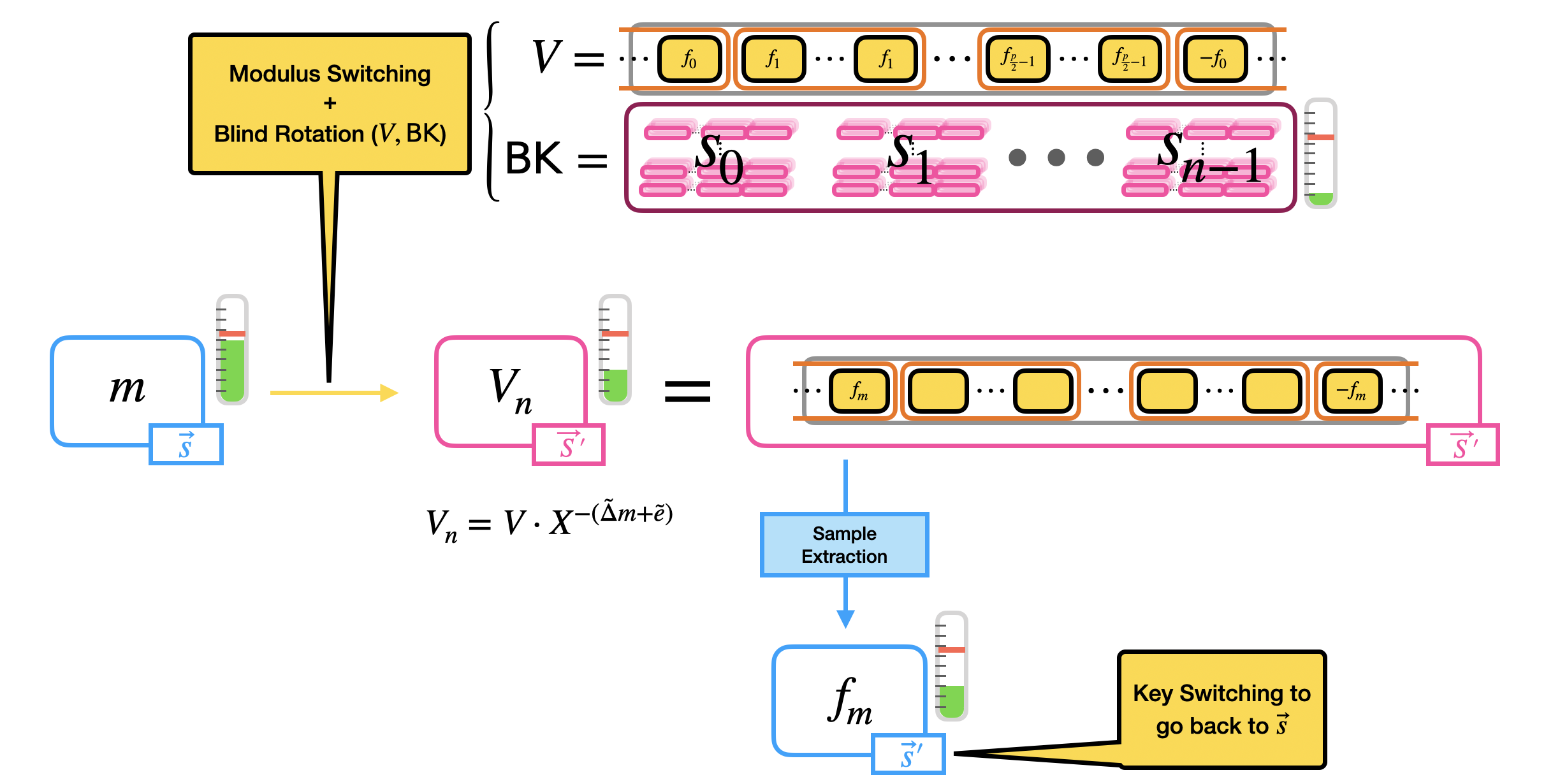
An example of bootstrapping: the Gate Bootstrapping

同态二元电路门，同时进行自举降低噪音。所有的电路门都可以被运算 (AND, NAND, OR, XOR, etc.)。以 AND 为例。

自举电路门输入两个 LWE 密文 $c_1, c_2$，在相同的密钥下加密两个 bits $\mu_1, \mu_2$。bit 信息以特殊的方式编码：0 编码为 $-q/8$，1 编码为 $q/8$。以下两个步骤：

对两个密文进行线性组合 (取决与要运算的电路门)。
自举 (并对输出更换为原密钥)，运算了编码为多项式 $V = \sum_{j=0}^{N-1} \frac{q}{8} X^j$ 的 LUT。这是一种变更缩放的符号函数，对所有正的消息输出 $q/8$，对所有负的消息输出 $-q/8$。这是负循环的函数所以不需要 1 bit 的 padding (?)。

自举可视化：

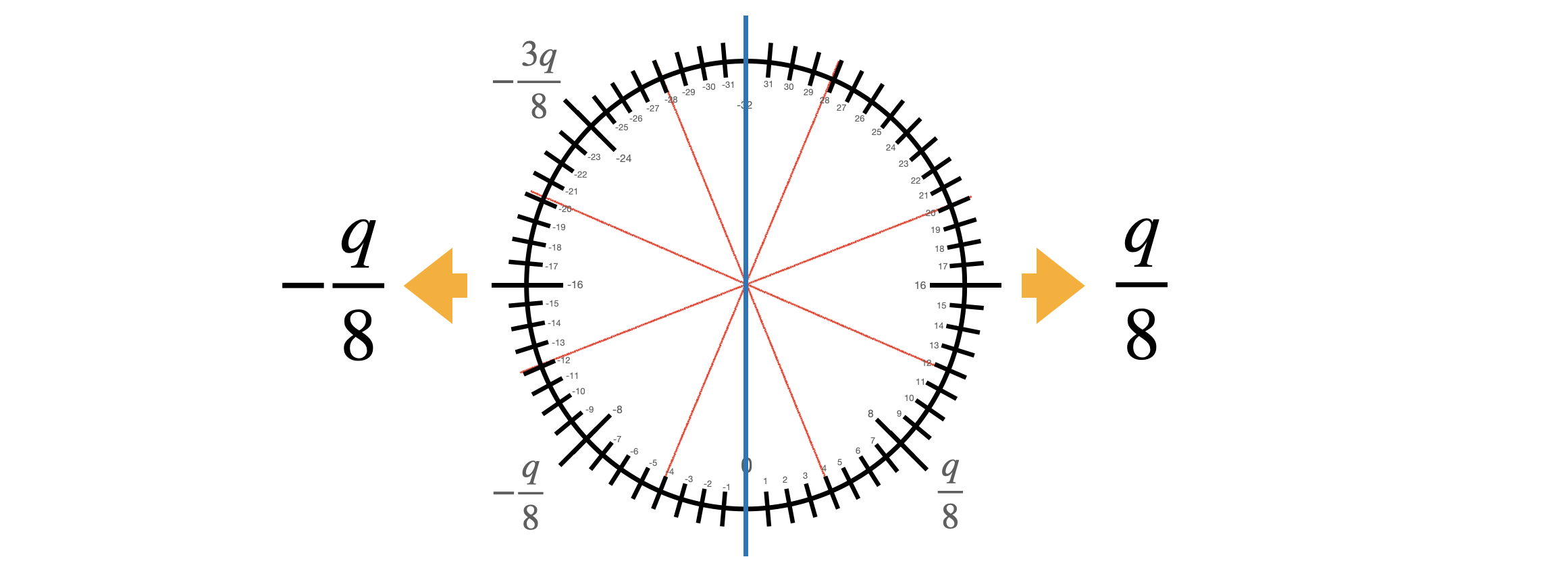
输出跟输入编码一样，可以直接传给第二个电路门。 o b$

对输出 $y$ 运算激活函数 $f$，非线性，如 ReLU，sigmoid, hyperbolic tangent 等。

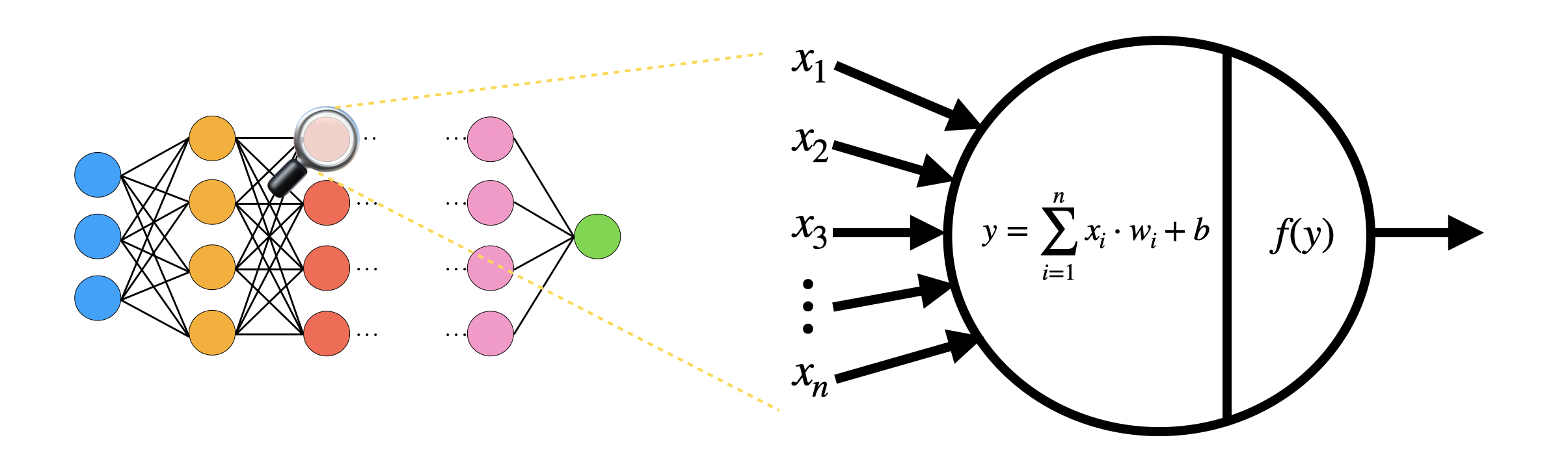
TFHE 可以同态的推理神经网络，加密输入 $x_i$ (最高大概 8 bits) 作为 LWE 输入，用数乘和 LWE 加法计算线性组合，激活函数以可编程自举计算，在降低噪音的同时输出可以给下一层神经元。可以计算任意，任何深度神经元。

TFHE

ドーナツ食べたくなった(*´_ゝ｀)