It sure is Cryptomania of my world!!!
--Just my wish
本篇开始咱想讲一讲咱对计算复杂性的浅显理解以及其为什么成为现代密码学的基石。计算复杂性理论相当重要且其理论仍在不断发展当中,千禧大奖问题和近些年麦琪奖的获奖论文都反应出其举足轻重的作用。说实话计算复杂性和安全性归约咱感觉相当抽象且难以理解,前前后后死了很多脑细胞,所得到的认知依然非常浅显。希望未来的咱有一天回顾以前的认知能直接笑死:“哈哈,傻逼!”
从完美安全到“实践”安全
密码学的时过境迁
咱都知道,密码学发展史上大家都会说有两个飞跃巅峰,第一次冲击飞跃是1949年香农发表了《保密系统的通信理论》Communication Theory of Secrecy Systems;第二个是1976年,Diffie和Hellman发表了《密码学的新方向》New Directions in Cryptography。
两篇文章咱都没看过(理直气壮。但一次性密码本(One-time pad)和公钥密码咱可是在熟悉不过了。一次性密码本可能有的人不太熟悉,毕竟以互联网通信为基础的现代密码学中对这种偏向于古典的替换密码使用的并不多(我认为,但很多人都认为这篇文章打开了现代密码学的大门。概述一下,香农1949年所发表的这篇文章从信息论的角度上探讨了密码学的安全性,提出了完善保密性(perfect secrecy)(信息论安全性(Information-theoretic security))的概念,分析了古典替换密码:一次性密码本,并提出了具有完善保密性的方案必须有和一次性密码本相同的的要求。完善保密性代表至高无上的安全性,即密文不泄露明文的任何信息。也就是说,拥有无限计算资源的敌手在无限时间内都无法以大于0的概率破解。听上去感觉很神秘,实际上这种安全性是基于信息论(概率论)的。
为什么完善保密性具有这么高的安全性但现在却很少被提及了呢?原因就是其代价太大了。对于一次性密码本来说,要达到完善保密性其密钥空间要大于明文空间,也就是密码本的尺寸要大于输入明文的尺寸。这确实是很难以实践运用的一个要求。因此,我们就会想到:也许密码方案达不到完善保密性也可以,只需要在实践层面上无法被“破解”就可以了。比如运行在神威·太湖之光的敌手无法在200年内破解某密码方案,是否就可以说这个方案无法被破解呢?依据着这个想法,密码学迎来第二个飞跃。
接下来让我们聊一聊第二个飞跃。相信大家都听说过公钥密码(这位更是重量级),实际上公钥密码从提出距今也只有40余年的历史,应该可以说是比较年轻的一个研究领域?实际上,Diffie和Hellman的文章除了提出了公钥密码这一新概念之外也为现代密码学引入了计算复杂性理论的概念(我只看了摘要),也就是今天的主题。

这里我画了张MIME图,表示我对密码学发展时过境迁的理解。看不懂是吧,我自己也看不懂。左边的巴别通天塔表示1976年之前的古典现代密码,其地基是信息论;右边的现代居民楼表示第二次飞跃之后的现代密码,其地基是计算复杂性理论。横坐标代表时间,其地基的变迁以1976年为分界点。纵坐标代表人们在对应年代对其安全性的定义,越高越安全。对于早期基于信息论的密码,以其能够达到完善保密性作为最高要求,所以我这里用古巴别通天塔代表其无限的高度。对于后期的现代密码人们只要求渐进的定义其安全性,于是我使用了居民楼的高度表示其安全性。居民楼毕竟没有宗教神话的高塔高,但更加实用,可以根据需求调节其高度,需要多高建多高。当然现代密码学里的一些组成部分也可以达到完善保密性,比如一定条件下的秘密共享方案和多方安全计算以及一些后量子密码等等,所以我对这两个建筑的纸面高度没有做太大区分。然而现代密码学的建设还没有完工,包括其地基计算复杂性理论的研究也并不完善(人们还不知道P是否等于NP),所以这栋居民楼还没有封顶,绝赞建设中。细心的人可能发现了居民楼的一部分有通天塔的影子,因为古典密码对现代密码的建设也产生了很多启发。特别是在块密码,流密码等密文密码领域。
渐进的安全性定义
以下章节可以参考”INTRODUCTION TO MODERN CRYPTOGRAPHY“Chapter 3。这本书也写的挺直观,
拉屎的时候可以读一读。
前请提要:如果不存在运行在神威·太湖之光的敌手算法在200年内“破解“某密码方案,也许就可以认为这个方案足够安全,因为这已经足够应对现实中可能出现的各种情况。但若其用超算连续计算了50年就能将其破解,难道这个密码方案就不安全了吗?或者是否存在一个人运气特别好,脸滚键盘就把密钥滚出来了呢?如何形式化定义这这些现实情况的安全性呢?
咱通过限制敌手的计算能力来定义安全性(毕竟无限制的敌手只有完善保密性不会被破解了),因此被称为“计算安全”。计算安全已经在事实上成为所有密码学安全被定义的方式,且有着严格的数学定义。但本博文不想深入探讨数学(主要是tex公式还没有完工(现在完工了,纪念一下下。还是主要探讨一下直观理解。计算安全性比起完美保密性放宽了的限制主要是有:
- 安全性只针对高效(多项式)敌手算法跑可行的时间。也就是说给他足够的时间就能暴力计算破解。但如果他暴力破解要的资源比如时间大于所有现实可能性,实践意义上便无法被破解。
- 敌手算法有很小的概率获胜(
脸滚键盘滚出密钥。如果这个概率足够小,同上。
结合以上思想,或许我们能具体分析一个方案的安全性。以下,第一种分析方法:
The Concrete Approach(具体分析)
定义走一走:
方案$(t, \varepsilon) \text {-secure }$如果敌手算法运行$t$时间内以最多$\varepsilon$的概率破解方案。
咱一般把敌手当成算法因为解决特定计算问题的都是计算机算法(总不会有人手算吧)。当然上述只是个模板,因为我们还没有定义怎样才算破解一个方案。这应对于咱期望方案满足的安全属性具体问题具体分析。举个栗子,某人有一个,能保证没有敌手算法,能在最高速的超级计算机上运行至多两百年,以比$2^{-60}$更高的概率,完全破解(逆向计算)此方案。或者不以时间而以CPU时钟进行计算,如至多$2^{80}$个时钟周期内。总之,最好能记住描述现代密码学安全定义的很大的数$t$,和很小的数$\varepsilon$。
运用具体分析方法的安全性保证在实践意义上非常重要,因为这是咱最终所关心的。然而具体的安全性保证非常难以得出。举个栗子,某方案声明没有敌手能在5年内以至多$\varepsilon$的概率破解此方案,敌手拥有怎样的算力?PC,超算还是全网所有计算机?5年有没有考虑到未来可能的算力提升?毕竟根据摩尔定理每18个月算力近似的会翻一倍。敌手算法是现成通用的,还是对此方案进行充分预处理的特化算法?就算这些问题都有详细的定义,这样一份具体的安全性保证也无法告诉咱敌手算法在2年内的成功概率以及超过5年比如10年后的成功概率。因此,咱可能会更偏向于采用第二种描述方法:
The Asymptotic Approach(渐进分析)
上面提到具体方法存在一些理论和技术问题,但是当咱对具体安全性没那么急切的要求时,不如使用更方便且抽象的分析方法,渐进地逼近安全性。这个方法基于计算复杂性理论,采用一个整数值的安全参数记作$n$,参数化了方案和参与的双方(挑战者和敌手)。挑战者初始化方案时会选择安全参数,方便理解这里就当成密钥长度。安全参数公开,我们现在再看看敌手的运行时间和成功概率,现在它们作为安全参数的函数而不是具体的数。然后:
- 视”高效的敌手”为运行时间多项式于$n$的概率性(randomized)算法。咱同时要求挑战者也运行在多项式时间内,尽管敌手可能比挑战者更为强大(运行时间也更长)。
- 视”可忽略的成功概率”小于任何多项式的逆。直观理解就是任何多项式算法无法对其进行逼近。相对应的名词有显著的(noticable)和压倒性的(overwelming)。
PPT意为“Probabilistic Polynomial-Time”(概率多项式时间)。一个渐进的安全性定义有以下通用形式:
若PPT敌手只能以可忽略的概率成功破解方案则方案安全。
因为这个安全概念取决于方案在足够大的安全参数值下的表现,所以咱将其称为渐进性的。关于渐进性的理解,整一波栗子:
假设咱有个渐进安全的方案,敌手运行$n^3$分钟内能以$2^{40}\cdot 2^{-n}$($n$的可忽略函数)”破解”这个方案。当$n\le 40$,意味着敌手跑$40^3$分钟(大概6周)就能够以概率1破解此方案。所以这个$n$没什么卵用。就算$n$取50敌手跑$50^3$(大概3个月)就能以大概千分之一的概率破解此方案,感觉还不太能接受。但是如果$n$取个500,敌手要跑200年才能以大概$2^{-500}$的概率破解此方案。
通过上面这个栗子,我们可以把安全参数看成一个拨杆让挑战者(一直觉得挑战者别扭,反正就是诚实阵营)自由调整自己的方案至期望的安全性,但增大安全参数同时使密钥变得更长,也降低了方案的运行效率,所以挑战者希望自己的安全参数越小越好,小到只要使方案满足他们关注的安全属性。实际上密钥长度是关于安全参数的多项式关系,咱简单定义了安全参数为密钥长度,就是想要说明对于敌手实施的攻击,比如密钥穷举攻击,所需要的时间随着密钥长度指数上升。通过安全参数增强方案安全性效果拔群,因为它帮助挑战者应对算力增长的敌手。再举个现实栗子:
假设咱有个方案,挑战者跑$10^{6}\cdot n^2$时钟周期,敌手跑$10^{8}\cdot n^4$时钟周期可以以最多$2^{-n/2}$概率“破解”此方案。考虑参与者都用的2GHz的计算机且挑战者确定安全参数为80,则挑战者要跑3.2秒,敌手跑3周内只能以$2^{-40}$的概率破解这个方案。假设哪一天有了8GHz的计算机,挑战者把安全参数设成160,这样能够维持3.2秒的运行时间,相反的,敌手却需要跑13周才能达到$2^{-80}$的成功概率。更快的计算机让敌手的工作变得更难了(其实是因为更高的安全参数)。
渐进逼近方案的安全性虽然方便简单,但在使用的时候需要注意:最终当一个方案落地,应用于实际场景时,依然需要一个具体的的安全性保证。但实际上,只要确定了安全参数,像上面一个例子一样,渐进安全分析就能够转换成具体的安全性保证。
归约
这部分可能会讲稍微多一点的数学记号,
感觉不涉及一点数学很难把这部分讲清楚。具体参考了”Mathematics of Public Key Cryptography“这本书可以说是相当规范的工具书了。闲着没事可以看看符号表。
前面章节给出了很多栗子,都体现了渐进方法和调整安全参数对方案安全性分析的重要作用。然而,上面这些例子都有一个前提条件。不妨假设敌手的破解概率为关于安全参数的函数$1/nlogn$(关于安全参数多项式变化),这样的敌手在安全参数增加时可能算的比方案的创建者还快,增加安全参数便完全起不到增加方案安全性的作用,反而会让方案变得更加低效。一个密码方案必须同时具备高效性和安全性,前者表明方案必须运行在输入参数的多项式时间内,后者则要求敌手对方案的”破解”必须与输入大小呈超多项式关系。那么如何去创建方案并证明其符合上述安全性呢?这又回到了计算复杂性理论上。
如果咱希望去证明一个给定的方案是计算安全的,就必须依靠尚未被证明的假设(除了信息论安全的情况)。咱的策略是去假设一些计算问题是困难的,或者一些底层的密码学原语是安全的(当然大前提建立在P≠NP上。),然后去证明在此假设下基于这些计算问题/原语的密码架构是安全的。咱通过归约来体现上述思想。一个明确的归约告诉我们如何将一个对密码方案进行攻击的敌手作为子程序用以解决困难问题。总的思想就是如果存在敌手能以不可忽略的概率$\varepsilon$”破解”一个密码方案实例,那么就存在另一个敌手以与$\varepsilon$多项式关系的概率(同样是不可忽略的)解决对应复杂问题的一个实例。因为我们假设的复杂问题是困难的,其在一些分布内均匀随机选择一个实例(假设其为平均情况困难问题),尚未被证明存在高效的(多项式的)算法能以不可忽略的概率解决对应实例,所以对应密码方案安全。下面给出归约在密码学中的数学定义:
问题A到问题B的归约是一个通过对问题B的谕言机(以不可忽略概率成功)进行访问的概率性算法(运行在expected polynomial-time(期望多项式时间)并有不可忽略的概率成功)来解决问题A
这里提到的期望多项式式时间是对概率性算法最坏情况复杂度的描述。如果存在这样一个从A到B的归约,咱把他记作:
\[A\leq_{R} B\]注意小于等于号右下角角标为R,意为randomized,为了与复杂性理论里的归约区分开。引理:
A和B为计算问题且$A\leq_{R} B$,如果存在B的概率多项式算法则存在A的概率多项式算法。
简单的说A不比B难(毕竟都记作小于等于号了)。如果问题B存在高效的解则问题A也存在高效的解。因为对谕言机的访问也需要一组运行时间,且归约是多项式时间算法,所以一个归约只能进行多项式次谕言机的访问。很多人容易把密码学的归约(reduction)和计算复杂性理论里的多项式归约(polynomial-time reduction)搞混,多项式归约小于等于号角标一般为P。技术层面上这两种说法指向的是不一样的东西,密码学里的归约更像CCT里的图灵归约一点,除了一个允许概率性算法一个是确定性算法。是不是已经被绕晕了,举个栗子:
咱可以建立一个从一元一次方程到一元二次方程的归约,只需要把一元二次方程的二次项系数设置为0,就可以将一元二次方程的解转换为对应一元一次方程的解。同样的,安全性证明需要创建一个从困难问题到密码方案的归约,是想要说明如果密码方案能够被高效破解,则困难问题也能被高效解决,用到了反证法的思想。一些密码学家可能习惯于在安全证明里面说某方案的安全性归约于某复杂问题。他们对”归约”一词的用法在算法理论上是错误的,他们可能是想要表达某方案的安全性基于某复杂问题。其安全性证明则要求从某复杂问题归约到密码方案(可能引起争议,放个链接。
一些概念与记法
多少放些定义,都是很基础的东西。
确定性算法
一个计算问题由满足一定形式的输入输出指定,且输出与输入满足特定的关联性。一个计算问题实例就是一个特定的输入。判定问题是输出只能为0或1的计算问题。没有任何随机性的算法叫做确定性算法,咱通过数他的位操作数(bit operations)分析其渐进复杂度并将其表示为输入大小的函数。一些渐进记号:渐进上界$O$,非渐进紧确上界$o$,渐进紧确界$\Theta$,渐进下界$\Omega$,非渐进紧确下界$\omega$等。常用的还有$\tilde{O}$,$f(n)=\tilde{O}(g(n)),i.e. f(n)=O\left(n \log (n)^{m}\right)$。各种记号的渐进思想如下图所示:
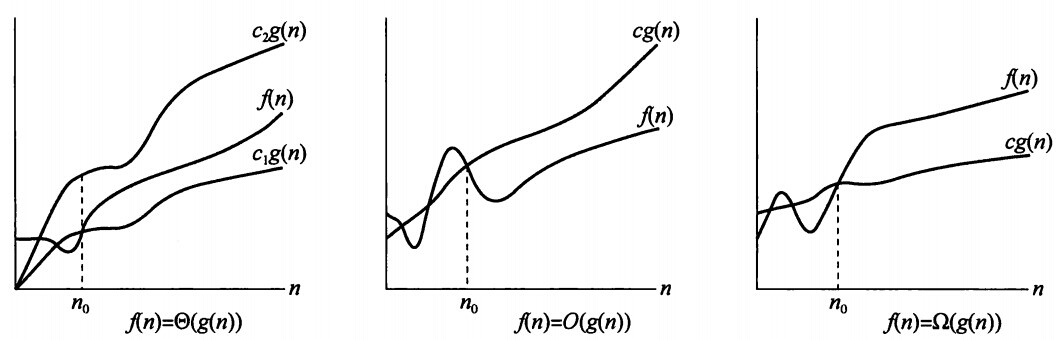
对于确定性问题的最坏情况渐进复杂度,如果其算法$A$能够解决这个计算问题的所有实例,就将其复杂度称为均匀复杂度(uniform complexity)。咱通常用关于输入大小的函数$t(n)$来描述其运行时间上界,一般有:
- polynomial-time(多项式时间),$\exists k\in \mathbb{N}:t(n)=O(n^k)$
- superpolynomial-time(超多项式时间),$\forall c\in \mathbb{R}_{>1},t(n)=\Omega (n^c)$
- exponential-time(指数时间),$\exists c_{2}>1:t(n)=O(c_{2}^n)$
- subexponential-time(亚指数时间),$\forall c\in \mathbb{R}_{>1},t(n)=O(c^n)$
咱也可以考虑非均匀复杂度(non-uniform complexity)的问题,其算法对于每一个不同输入长度的实例都需要一个hint辅助运算。也就是做不到一招鲜吃遍天。
概率性算法
密码学里绝大部分算法都是概率性算法。概率性算法的定义涉及到其运行每一步对随机比特生成器的访问,咱不妨从其性质理解概率性算法,其两个性质:
- 如果其随机数的选择相当不幸,可能会永远运行下去。但在密码学中对其运行时间上限进行约束一般情况下是必要的。
- 概率性算法每次运行输出都不一样,且可能输出期望之外的错误结果。比如解密算法的$\bot$。
概率性算法有两个非常典型的例子可以帮助理解这两个性质:拉斯维加斯算法(Las Vegas algorithm)和蒙地卡罗算法(Monte Carlo algorithm)。拉斯维加斯算法仅在输出正确结果时终止;蒙地卡罗算法作为判定性算法运用统计方法解决计算问题,如果其总是终止且输出为1则其输出正确结果,如果输出为0则其以显著的概率输出正确结果。
复杂度类
P:存在多项式算法。如解一元二次方程 NP:存在多项式验证法。如验证某数是否是素数 NP-hard:任何多项式问题都可多项式归约至此类问题 NP-completeness:是NP问题且是NP-hard问题。解决一个此类问题即解决了所有NP问题。

姑且先讲这么多,下一篇见。