方格填数
如下的10个格子
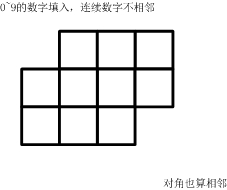
填入0~9的数字。要求:连续的两个数字不能相邻。 (左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
慎用全局变量
这题本身没啥问题,但代码自信满满写出来之后,编译运行却什么结果都没有显示,仔细检查了好几遍逻辑也没有什么错误。网上找来了别人的参考答案对比了一下跟自己也差不多,而他的却可以运行出正确结果,十分不解。
实在找不到错误,GDB走起。
我将正确答案和自己的答案同时编译出来,一个窗口上逐行调试,最终发现自己的程序运行到一半就直接退出了,没有报任何错误,而且所执行的代码跟正确答案的代码也一模一样,如下图所示:

左下角面板里是我的版本,左上角是网上的版本。可以看到左下角在调用 dfs(2,1) 时意外退出了。
当时还是不知道原因,后来上课时我在手机上用GDB调试,发现递归函数没有正确return。监视了变量的值,才发现退出视里层函数结束时没有将k值归位,导致函数意外退出。
和正确答案对比了一下才发现自己的变量声明的是全局变量,而对于递归调用声明全局变量时需要层层将其归位,一般声明成局部变量更加方便并且不容易出错。
代码
#include<bits/stdc++.h>
using namespace std;
int sum;
int a[4][4];
int used[100];
void display(){
cout<<sum<<" *"<<endl;
for(int i=0;i<2;i++){
for(int j=0;j<3;j++){
cout<<a[i][j]<<' ';
}
cout<<endl;
}
cout<<endl;
}
/*int k;//定义全局变量不可用
int mi,mj;
int mmi,mmj;
bool flag;*/
void dfs(int i,int j){
if(i==2&&j==3){
sum++;
display();
return;
}
int k;
int mi,mj;
int mmi,mmj;
bool flag;
for(k=0;k<10;k++){
if(used[k])continue;
flag=true;
for(mi=-1;mi<=1;mi++){
for(mj=-1;mj<=1;mj++){
mmi=i+mi;
mmj=j+mj;
if(mmi>=0&&mmi<=2 && mmj>=0&&mmj<=3){
if(a[mmi][mmj]!=-1){
if(abs(a[mmi][mmj]-k)==1){
flag=false;
}
}
}
}
}
if(flag){
a[i][j]=k;
used[k]=true;
if(j==3){
dfs(i+1,0);
}else{
dfs(i,j+1);
}
a[i][j]=-1;
used[k]=false;
}
}
}
int main(){
memset(used,false,sizeof(used));
memset(a,-1,sizeof(a));
sum=0;
dfs(0,1);
return 0;
}
next_permutation版本
#include<bits/stdc++.h>
using namespace std;
int main(){
int num=0;
int a[10]={
0,1,2,3,4,5,6,7,8,9
};
do{
if(abs(a[0]-a[1])==1||abs(a[0]-a[3])==1||abs(a[0]-a[4])==1||abs(a[0]-a[5])==1)
continue;
if(abs(a[1]-a[2])==1||abs(a[1]-a[4])==1||abs(a[1]-a[5])==1||abs(a[1]-a[6])==1)
continue;
if(abs(a[2]-a[5])==1||abs(a[2]-a[6])==1)
continue;
if(abs(a[3]-a[4])==1||abs(a[3]-a[7])==1||abs(a[3]-a[8])==1)
continue;
if(abs(a[4]-a[5])==1||abs(a[4]-a[7])==1||abs(a[4]-a[8])==1||abs(a[4]-a[9])==1)
continue;
if(abs(a[5]-a[6])==1||abs(a[5]-a[8])==1||abs(a[5]-a[9])==1)
continue;
if(abs(a[6]-a[9])==1)
continue;
if(abs(a[7]-a[8])==1)
continue;
if(abs(a[8]-a[9])==1)
continue;
num++;
}while(next_permutation(a,a+10));
cout<<num<<endl;
return 0;
}